+/- r Code
+/- r Code
+/- r Code
Quantitative Big Imaging
author: Kevin Mader date: 16 April 2015 width: 1440 height: 900 css: ../common/template.css transition: rotate
ETHZ: 227-0966-00L
Groups of Objects and Distributions
Course Outline
+/- r Code
- 19th February - Introduction and Workflows
- 26th February - Image Enhancement (A. Kaestner)
- 5th March - Basic Segmentation, Discrete Binary Structures
- 12th March - Advanced Segmentation
- 19th March - Applying Graphical Models and Machine Learning (A. Lucchi)
- 26th March - Analyzing Single Objects
- 2nd April - Analyzing Complex Objects
- 16th April - Spatial Distribution
- 23rd April - Statistics and Reproducibility
- 30th April - Dynamic Experiments (K. Mader and A. Patera)
- 7th May - Scaling Up / Big Data
- 21th May - Guest Lecture, Applications in Material Science
- 28th May - Project Presentations
Literature / Useful References
Books
- Jean Claude, Morphometry with R
- John C. Russ, “The Image Processing Handbook”,(Boca Raton, CRC Press)
- Available online within domain ethz.ch (or proxy.ethz.ch / public VPN)
- J. Weickert, Visualization and Processing of Tensor Fields
Papers / Sites
Voronoi Tesselations
- Ghosh, S. (1997). Tessellation-based computational methods for the characterization and analysis of heterogeneous microstructures. Composites Science and Technology, 57(9-10), 1187–1210
- Wolfram Explanation
Self-Avoiding / Nearest Neighbor
- Schwarz, H., & Exner, H. E. (1983). The characterization of the arrangement of feature centroids in planes and volumes. Journal of Microscopy, 129(2), 155–169.
- Kubitscheck, U. et al. (1996). Single nuclear pores visualized by confocal microscopy and image processing. Biophysical Journal, 70(5), 2067–77.
Alignment / Distribution Tensor
- Mader, K. et al (2013). A quantitative framework for the 3D characterization of the osteocyte lacunar system. Bone, 57(1), 142–154
- Aubouy, M., et al. (2003). A texture tensor to quantify deformations. Granular Matter, 5, 67–70. Retrieved from http://arxiv.org/abs/cond-mat/0301018
Two point correlation
- Dinis, L., et. al. (2007). Analysis of 3D solids using the natural neighbour radial point interpolation method. Computer Methods in Applied Mechanics and Engineering, 196(13-16)
Previously on QBI ...
- Image Enhancment
- Highlighting the contrast of interest in images
- Minimizing Noise
- Understanding image histograms
- Automatic Methods
- Component Labeling
- Single Shape Analysis
- Complicated Shapes
Outline
- Motivation (Why and How?)
- Local Environment
- Neighbors
- Voronoi Tesselation
- Distribution Tensor
- Global Enviroment
- Alignment
- Self-Avoidance
- Two Point Correlation Function
Metrics
We examine a number of different metrics in this lecture and additionally to classifying them as Local and Global we can define them as point and voxel-based operations.
Point Operations
- Nearest Neighbor
- Delaunay Triangulation
- Distribution Tensor
- Point (Center of Volume)-based Voronoi Tesselation
- Alignment
+/- r Code
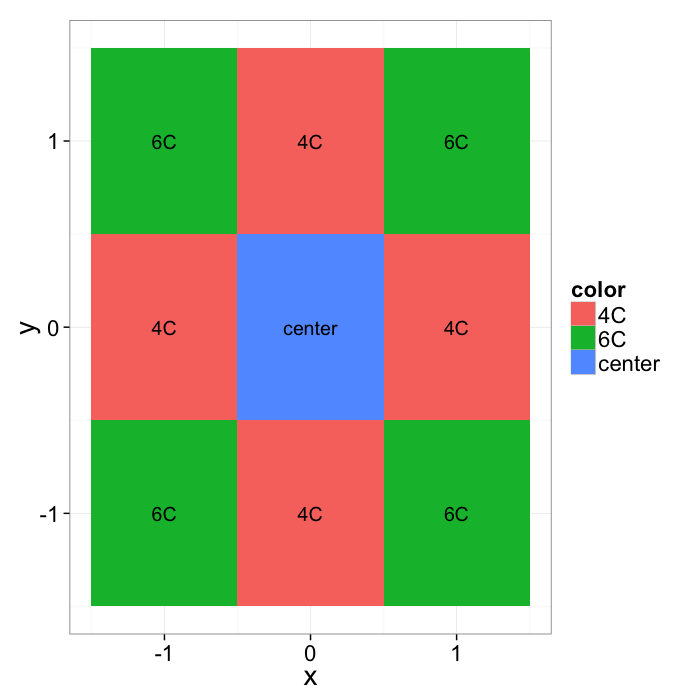
| x | y | z |
|---|---|---|
| 1 | 3 | 4 |
| 2 | 0 | 2 |
| 2 | 3 | 2 |
| 3 | 1 | 4 |
Voxel Operation
- Voronoi Tesselation
- Neighbor Counting
- 2-point (N-point) correlation functions
What do we start with?
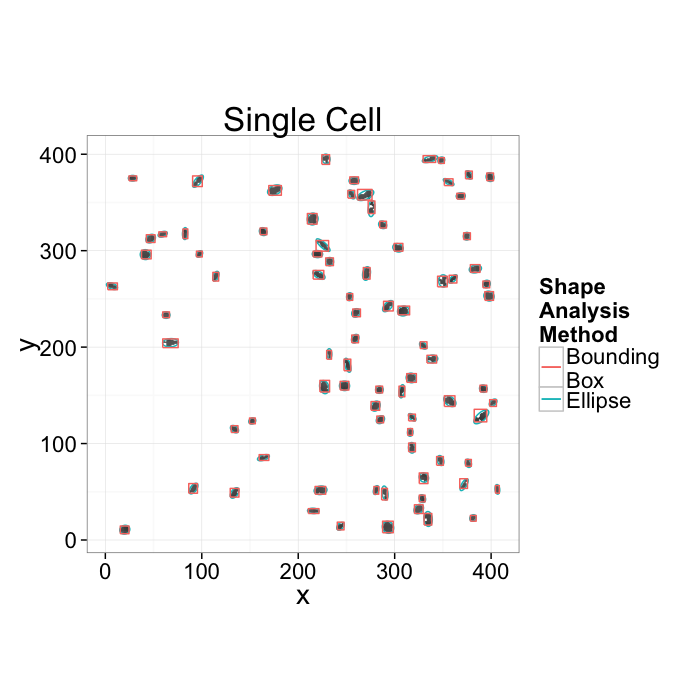
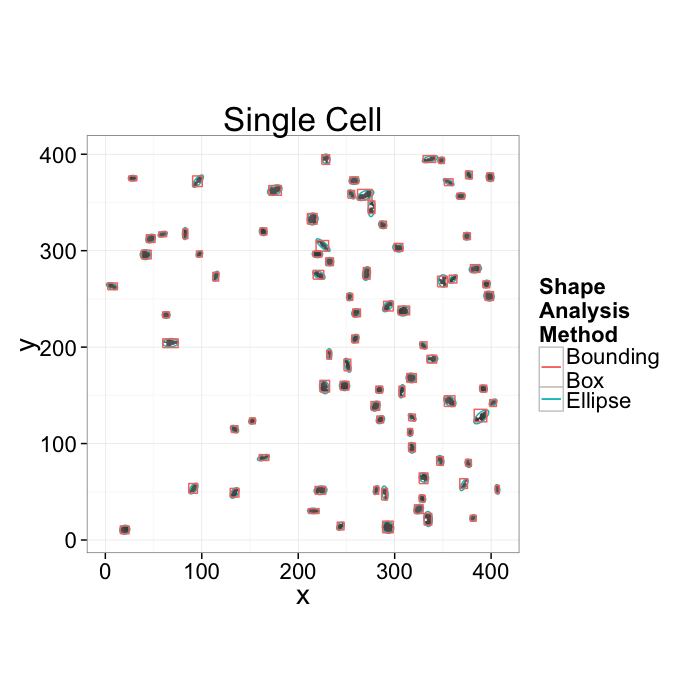
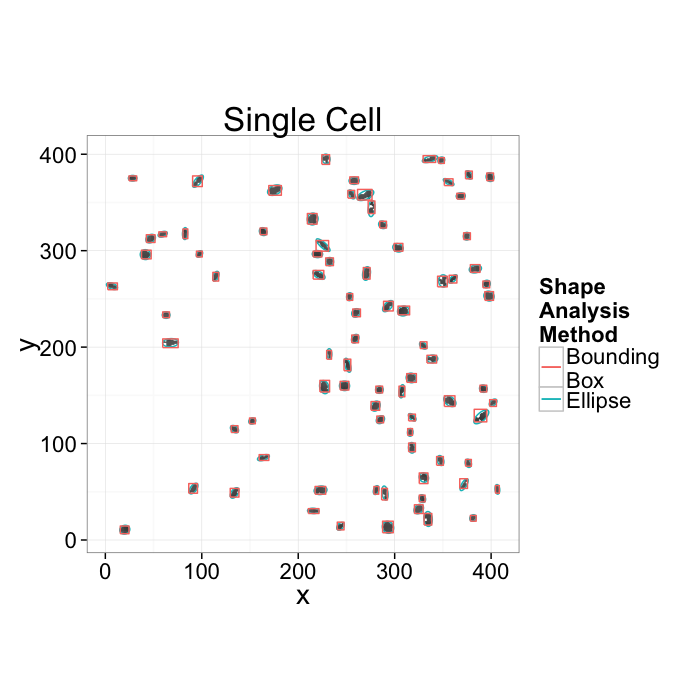
Going back to our original cell image
- We have been able to get rid of the noise in the image and find all the cells (lecture 2-4)
- We have analyzed the shape of the cells using the shape tensor (lecture 5)
- We even separated cells joined together using Watershed (lecture 6)
We can characterize the sample and the average and standard deviations of volume, orientation, surface area, and other metrics
Motivation (Why and How?)
With all of these images, the first step is always to understand exactly what we are trying to learn from our images.
We want to know how many cells are alive
- Maybe small cells are dead and larger cells are alive → examine the volume distribution
- Maybe living cells are round and dead cells are really spiky and pointy → examine anisotropy
We want to know where the cells are alive or most densely packed
- We can visually inspect the sample (maybe even color by volume)
- We can examine the raw positions (x,y,z) but what does that really tell us?
- We can make boxes and count the cells inside each one
- How do we compare two regions in the same sample or even two samples?
Motivation (continued)
- We want to know how the cells are communicating
- Maybe physically connected cells (touching) are communicating → watershed
- Maybe cells oriented the same direction are communicating → average? orientation
- Maybe cells which are close enough are communicating → ?
- Maybe cells form hub and spoke networks → ?
Motivation (continued)
- We want to know how the cells are nourished
- Maybe closely packed cells are better nourished → count cells in a box?
- Maybe cells are oriented around canals which supply them → ?
So what do we still need
- A way for counting cells in a region and estimating density without creating arbitrary boxes
- A way for finding out how many cells are near a given cell, it's nearest neighbors
- A way for quantifying how far apart cells are and then comparing different regions within a sample
- A way for quantifying and comparing orientations
What would be really great?
A tool which could be adapted to answering a large variety of problems
- multiple types of structures
- multiple phases
Destructive Measurements
With most imaging techniques and sample types, the task of measurement itself impacts the sample.
- Even techniques like X-ray tomography which claim to be non-destructive still impart significant to lethal doses of X-ray radition for high resolution imaging
- Electron microscopy, auto-tome-based methods, histology are all markedly more destructive and make longitudinal studies impossible
- Even when such measurements are possible
- Registration can be a difficult task and introduce artifacts
Why is this important?
- techniques which allow us to compare different samples of the same type.
- are sensitive to common transformations
- Sample B after the treatment looks like Sample A stretched to be 2x larger
- The volume fraction at the center is higher than the edges but organization remains the same
Ok, so now what?
↓
+/- r Code
| x | y | vx | vy |
|---|---|---|---|
| 20.19 | 10.69 | -0.95 | -0.30 |
| 20.19 | 10.69 | 0.30 | -0.95 |
| 293.08 | 13.18 | -0.50 | 0.86 |
| 293.08 | 13.18 | -0.86 | -0.50 |
| 243.81 | 14.23 | 0.68 | 0.74 |
| 243.81 | 14.23 | -0.74 | 0.68 |
⋯
So if we want to know the the mean or standard deviations of the position or orientations we can analyze them easily.
+/- r Code
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. | |
|---|---|---|---|---|---|---|
| x | 6.90 | 215.70 | 280.50 | 258.20 | 339.00 | 406.50 |
| y | 10.69 | 111.60 | 221.00 | 208.60 | 312.50 | 395.20 |
| Length | 1.06 | 1.57 | 1.95 | 2.08 | 2.41 | 4.33 |
| vx | -1.00 | -0.94 | -0.70 | -0.42 | 0.07 | 0.71 |
| vy | -1.00 | -0.70 | 0.02 | 0.04 | 0.71 | 1.00 |
| Theta | -180.00 | -134.10 | -0.50 | -4.67 | 130.60 | 177.70 |
- But what if we want more or other information?
Simple Statistics
When given a group of data, it is common to take a mean value since this is easy. The mean bone thickness is 0.3mm. This is particularly relevant for groups with many samples because the mean is much smaller than all of the individual points.
but means can lie
- the mean of 0∘ and 180∘ = 90∘
- the distance between -180∘ and 179∘ is 359∘
- since we have not defined a tip or head, 0∘ and 180∘ are actually the same
some means are not very useful
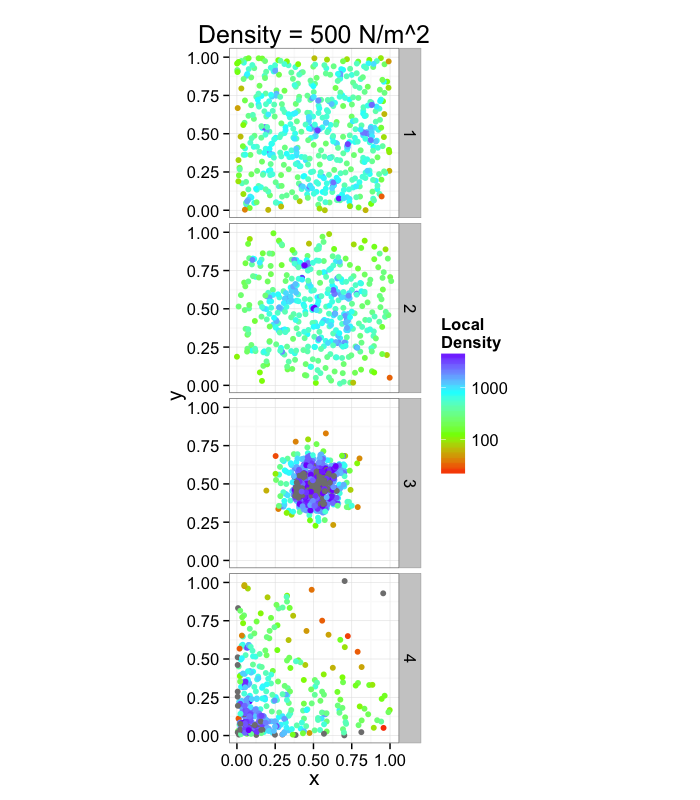
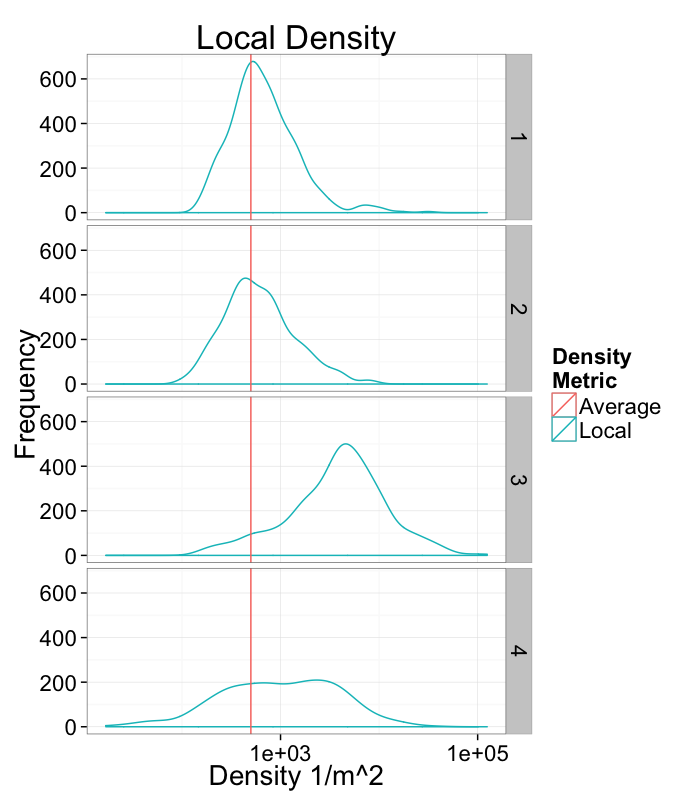
Calculating Density
One of the first metrics to examine with distribution is density → how many objects in a given region or volume.
It is deceptively easy to calculate involving the ratio of the number of objects divided by the volume.
It doesn't tell us much, many very different systems with the same density and what if we want the density of a single point? Does that even make sense?
Neighbors
Definition
Oxford American → be situated next to or very near to (another)
- Does not sound very scientific
- How close?
- Touching, closer than anything else?
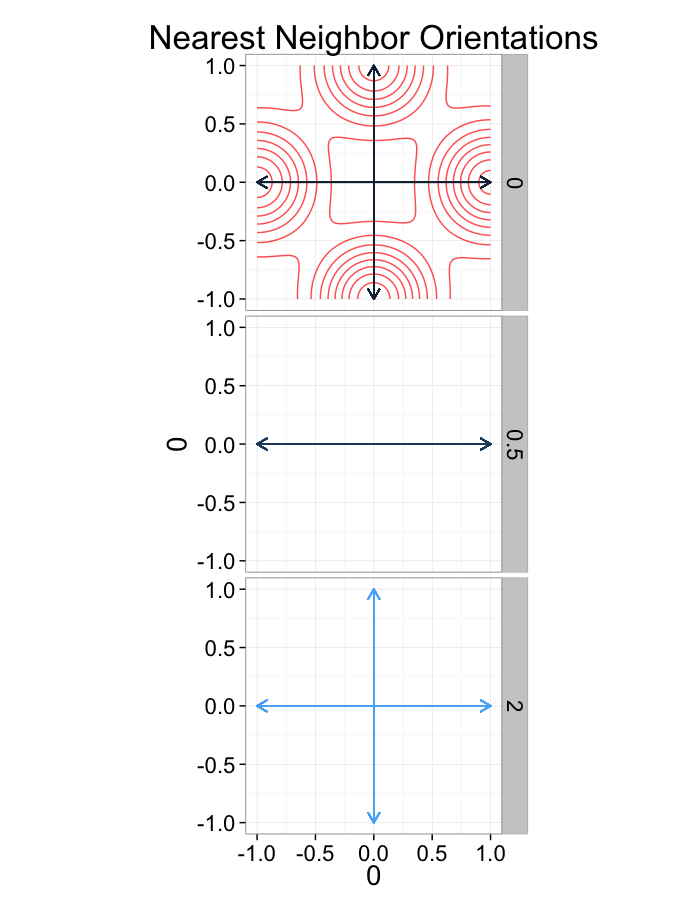
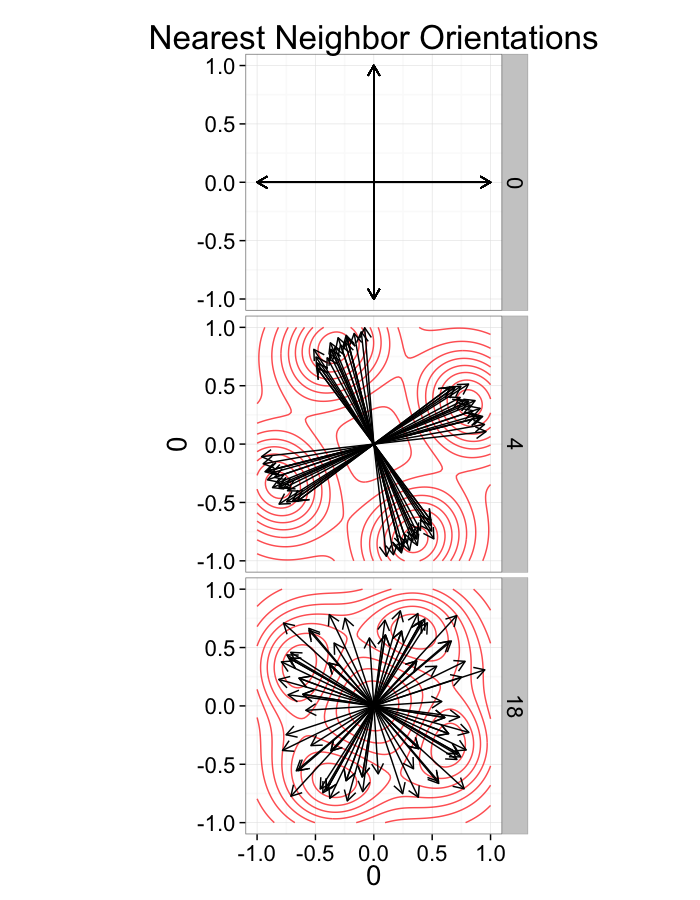
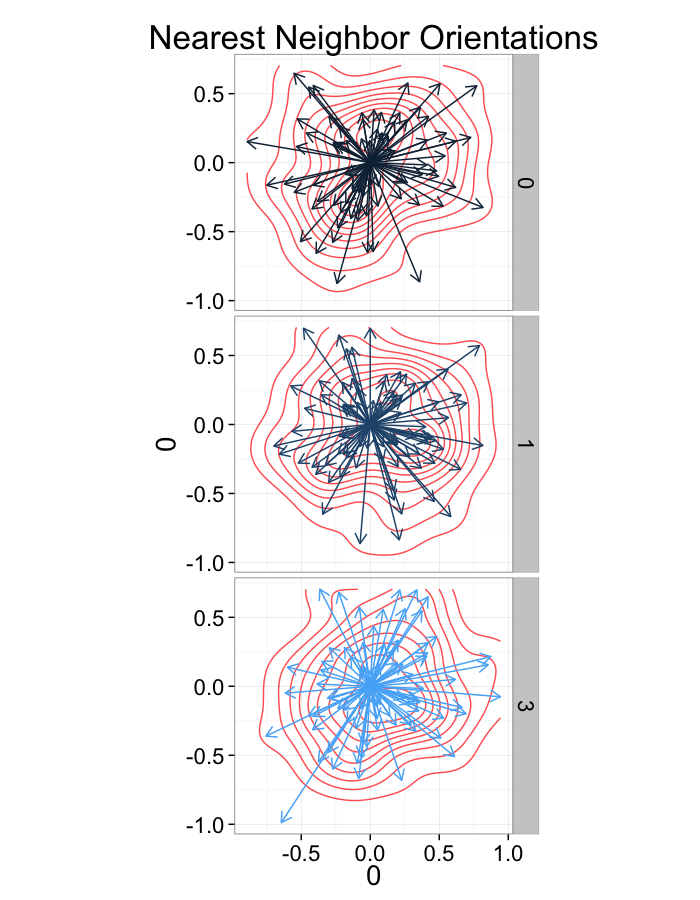
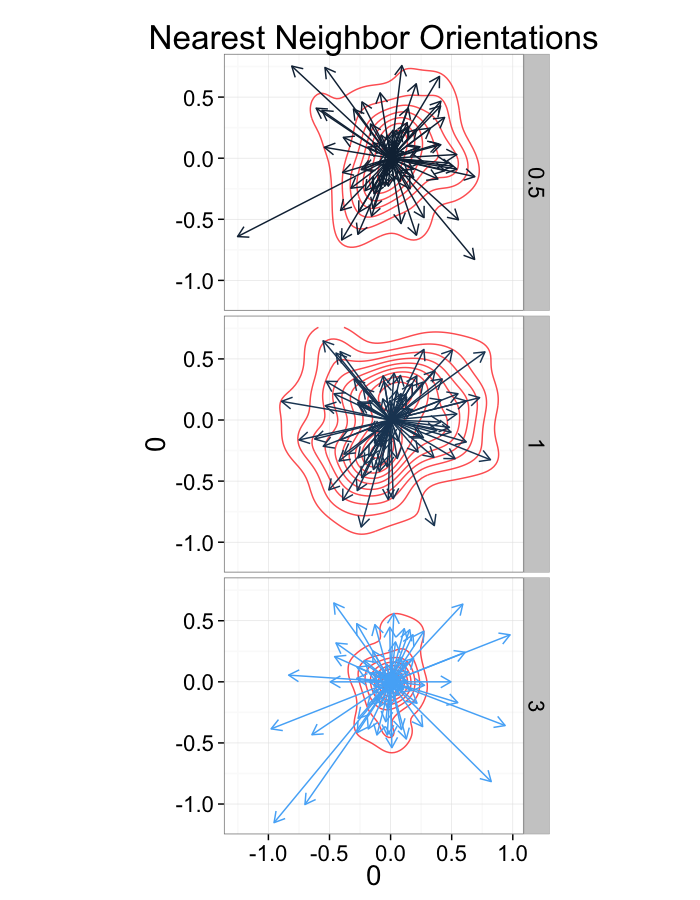
Nearest Neighbor (distance)
+/- r Code
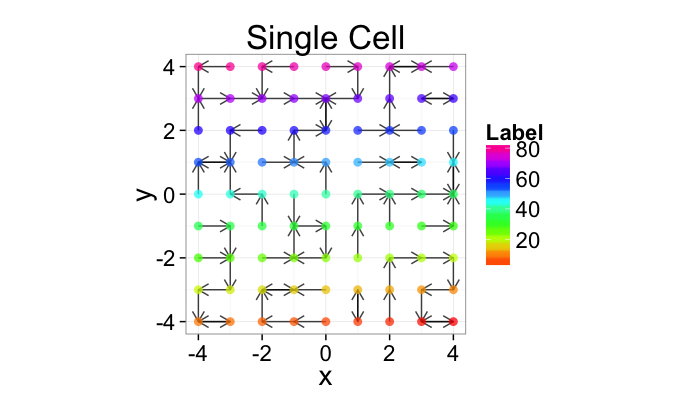
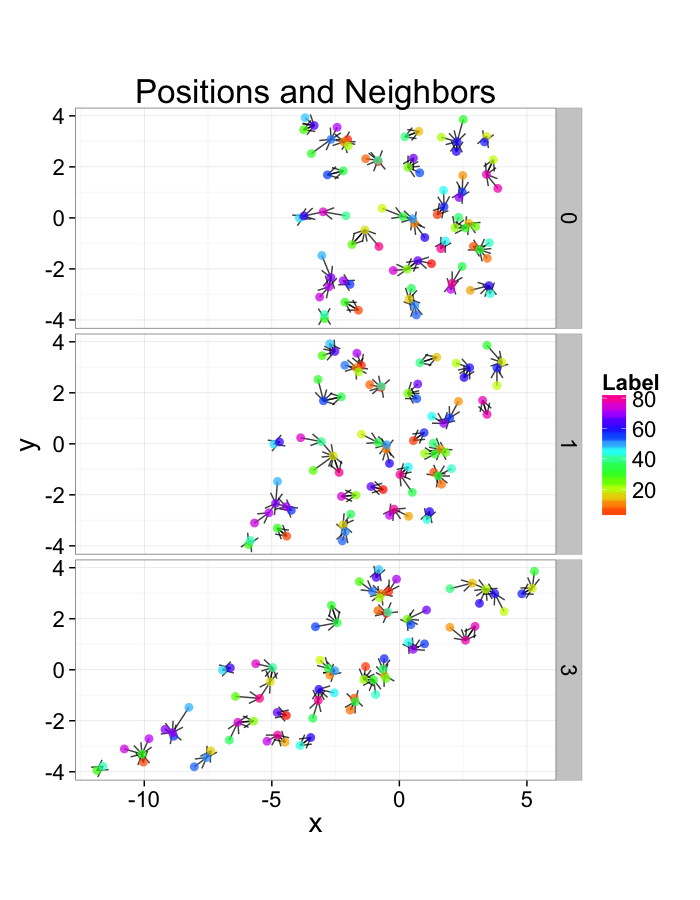
We can define the nearest neighbor as the position of the object in our set which is closest
→NN(→y)=argmin(||→y−→x||∀→x∈P−→y)
We define the distance as the Euclidean distance from the current point to that point, and the angle as the
NND(→y)=min(||→y−→x||∀→x∈P−→y) NNθ(→y)=tan−1(→NN−→y)⋅→j(→NN−→y)⋅→i
Nearest Neighbor Definition
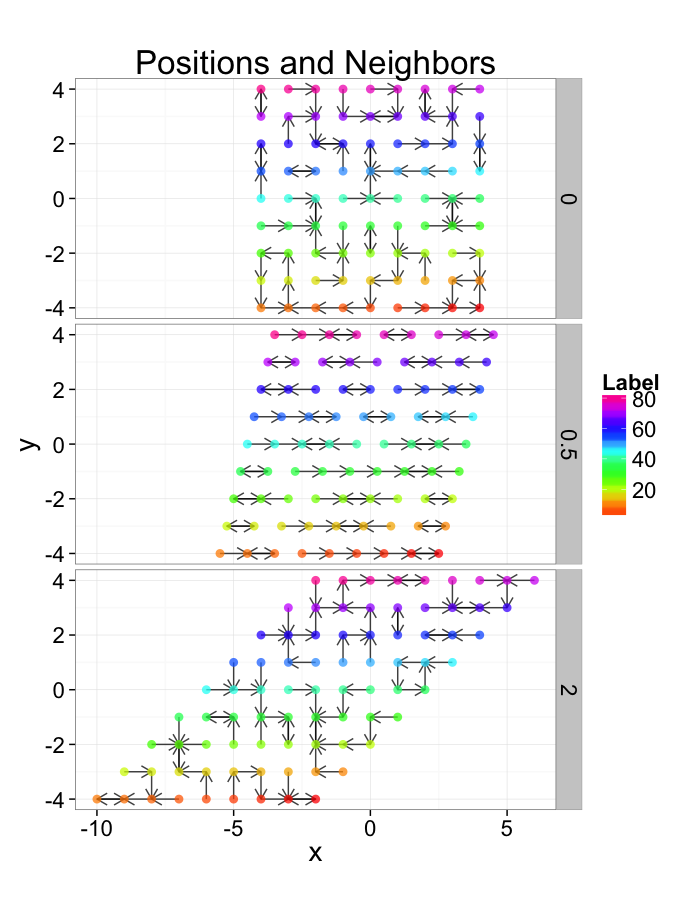
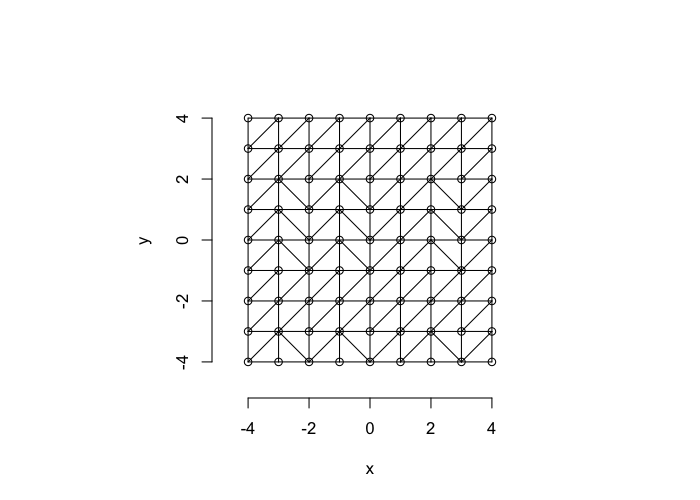
So examining a simple starting system like a grid, we already start running into issues.
- In a perfect grid like structure each object has 4 equidistant neighbors (6 in 3D)
- Which one is closest?
We thus add an additional clause (only relevant for simulated data) where if there are multiple equidistant neighbors, a nearest is chosen randomly
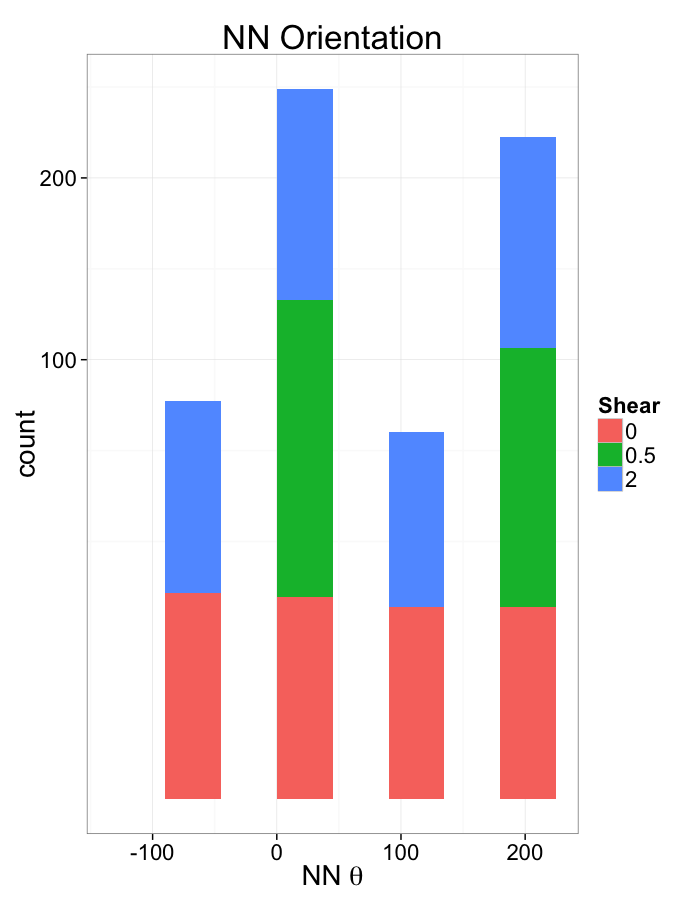
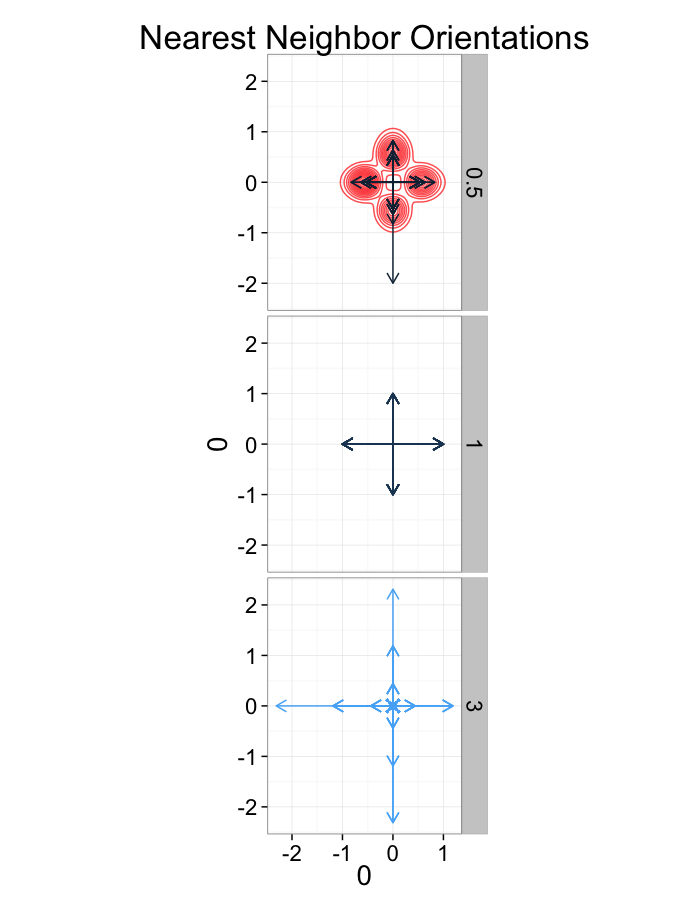
This ensures when we examine the orientation distribution (NNθ) of the neighbors it is evenly distributed
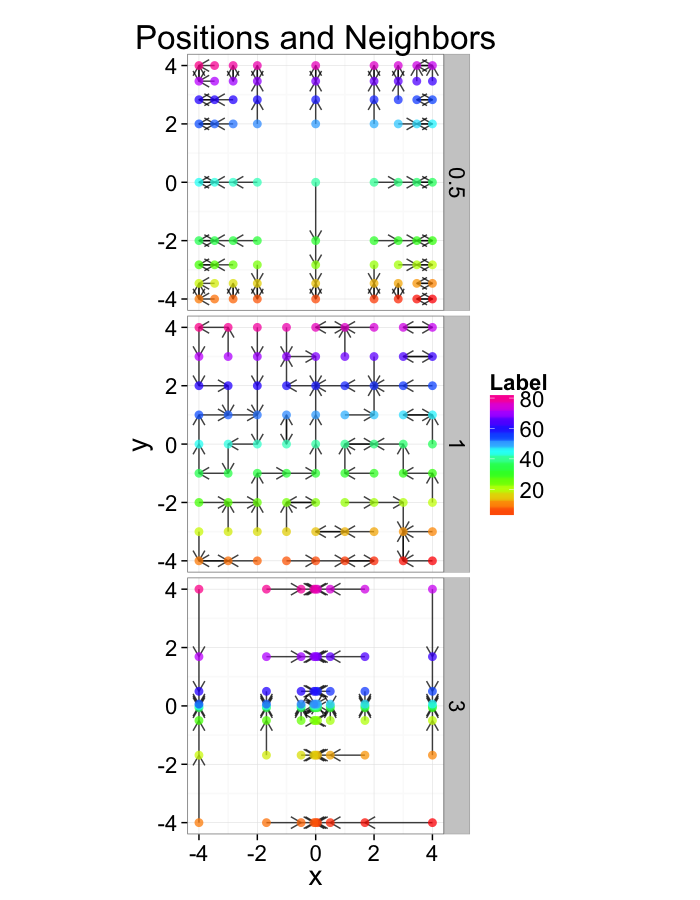
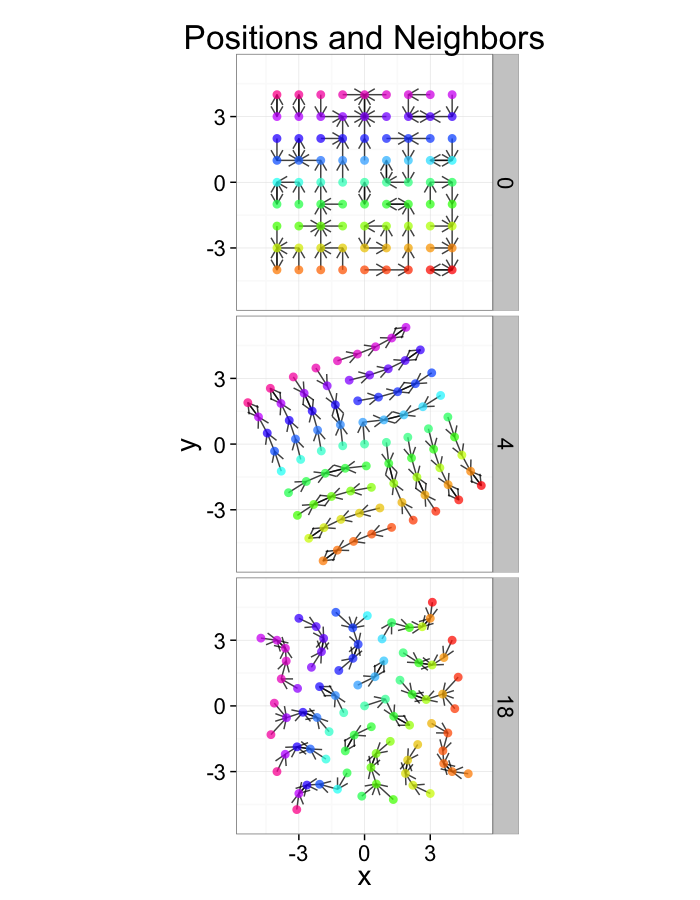
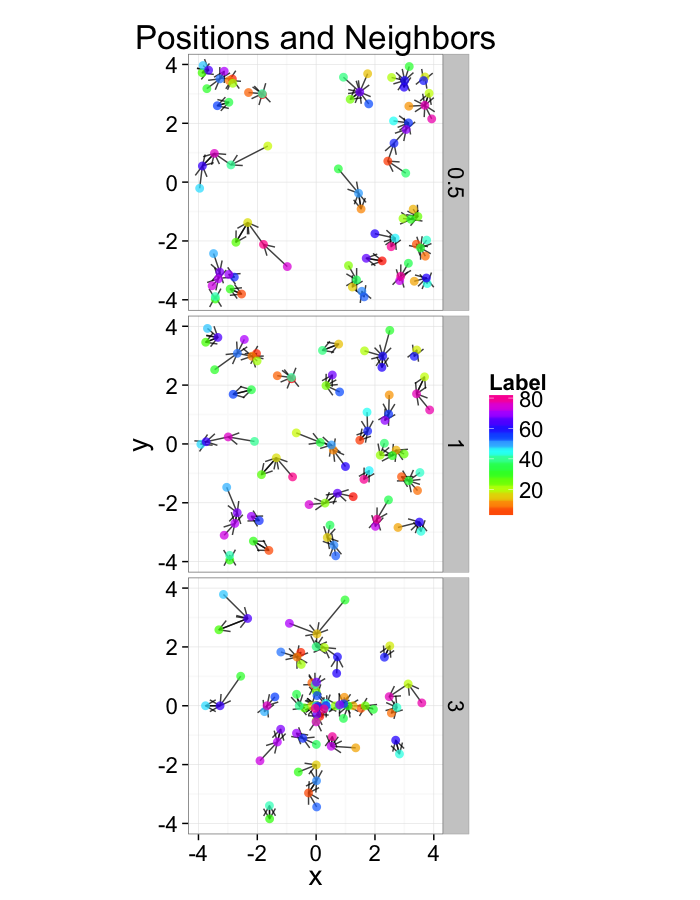
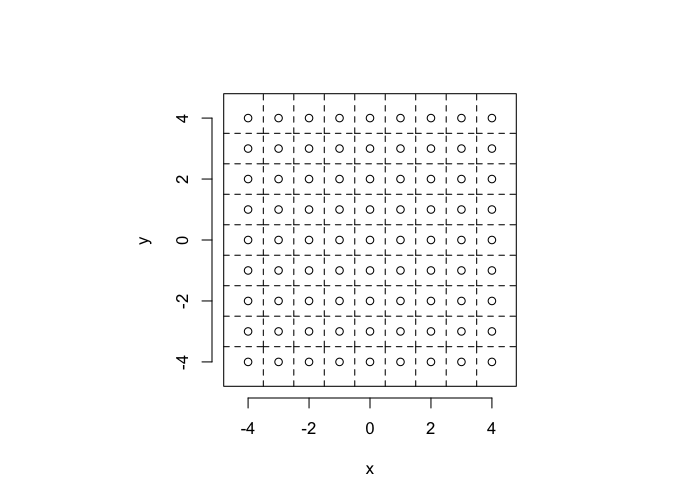
In-Silico Systems
For the rest of these sections we will repeatedly use several simple in-silico systems to test our methods and try to better understand the kind of results we obtain from them.
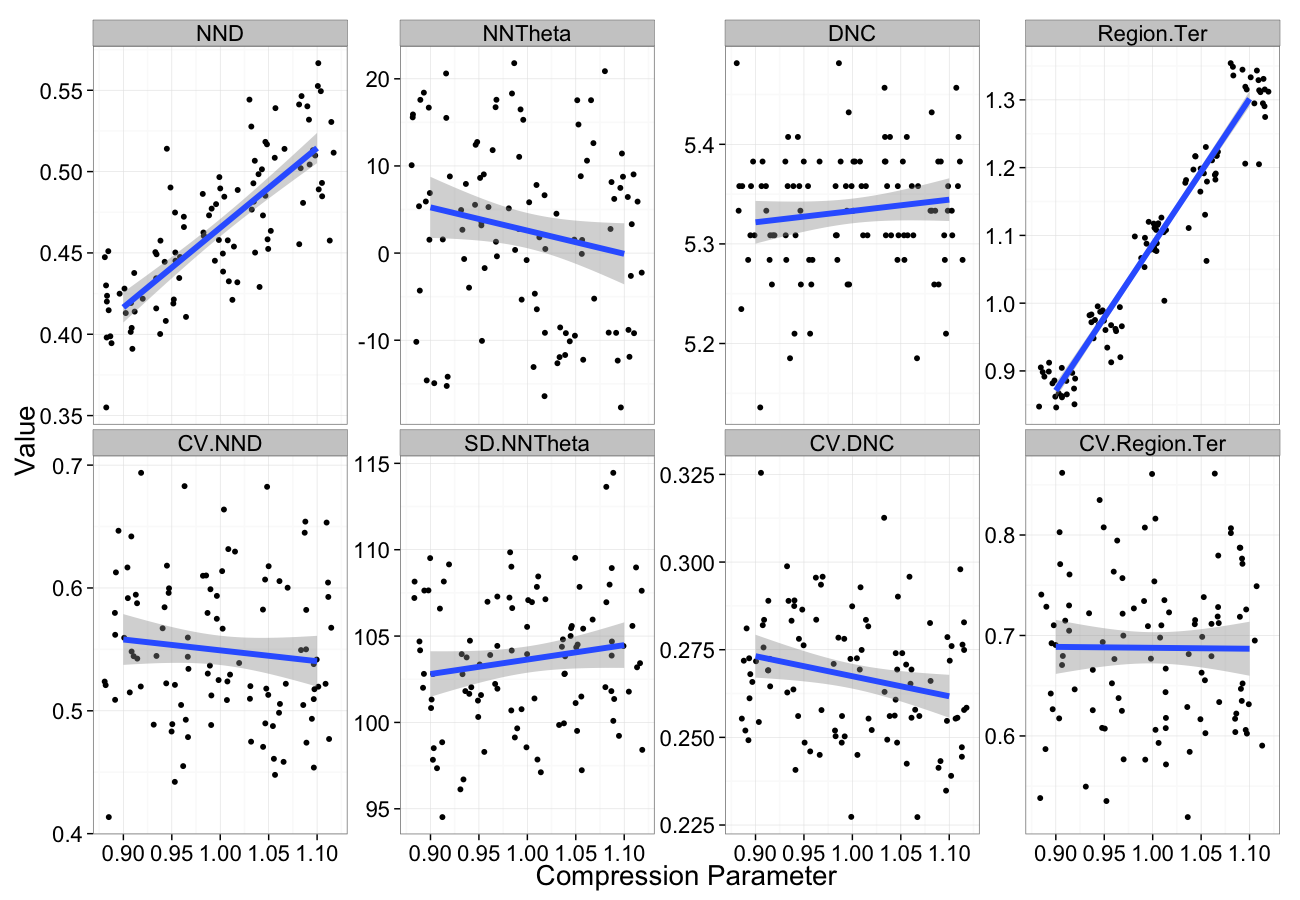
Compression
- The most simple system simply involves a scaling in every direction by α
- α<1 the system is compressed
- α>1 the system is expanded
[x′y′]=α[xy]
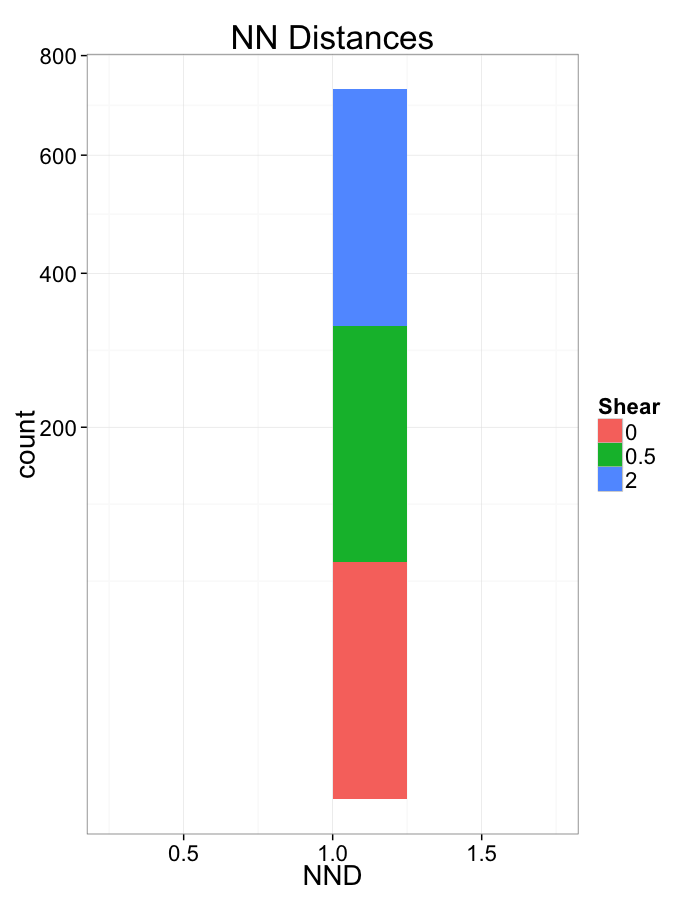
Shearing
- Slightly more complicated system where objects are shifted based on their location using a slope of α
[x′y′]=[1α01][xy]
In-Silico Systems (Continued)
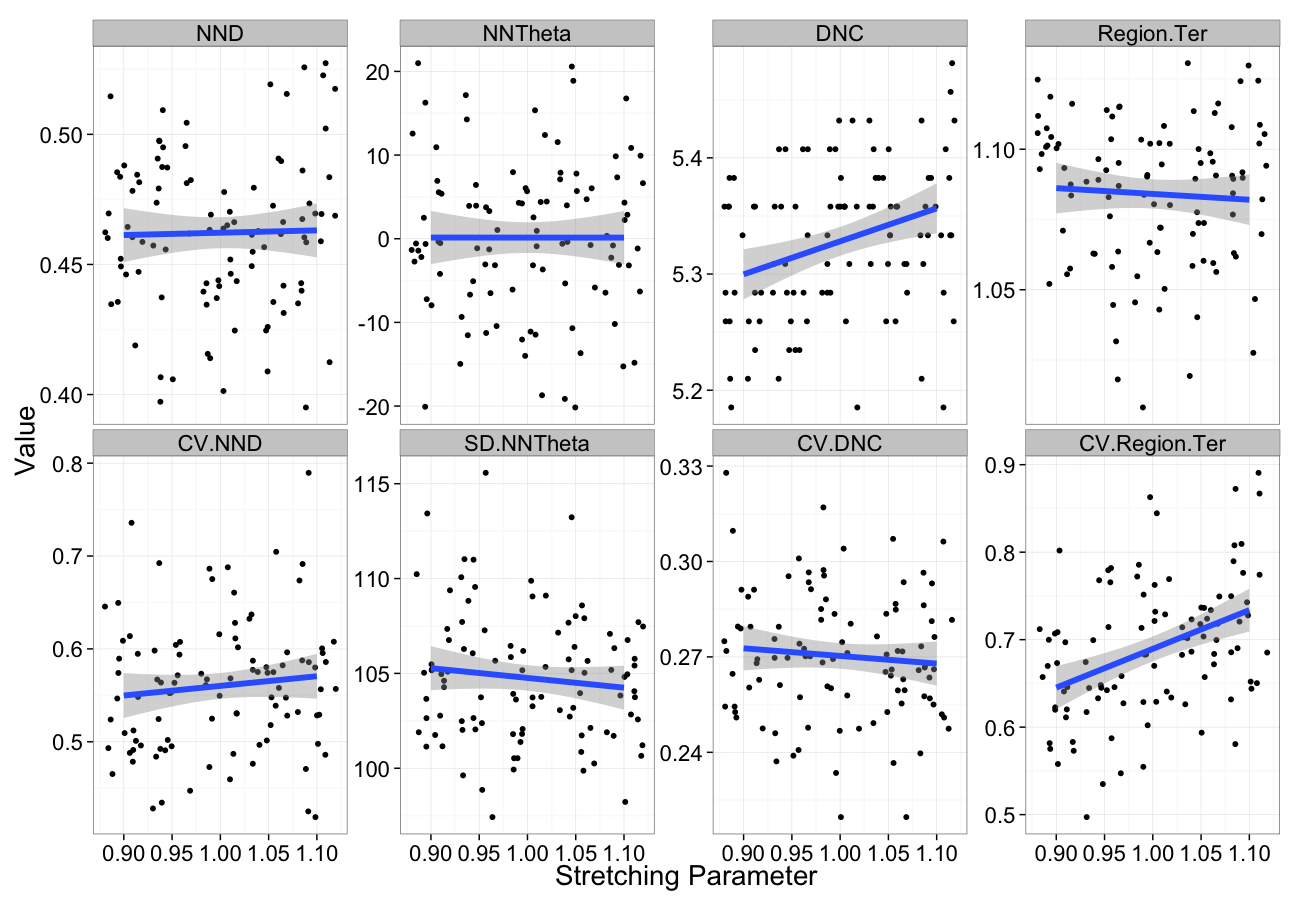
- Stretch
- A non-evenly distributed system with a parameter α controlling if objects bunch near the edges or the center. A maximum distance m is defined as the magnitude of the largest offset in x or y
- + Same total volume just arranged differently
[x′y′]=[sign(x)(|x|m)αmsign(y)(|y|m)αm]
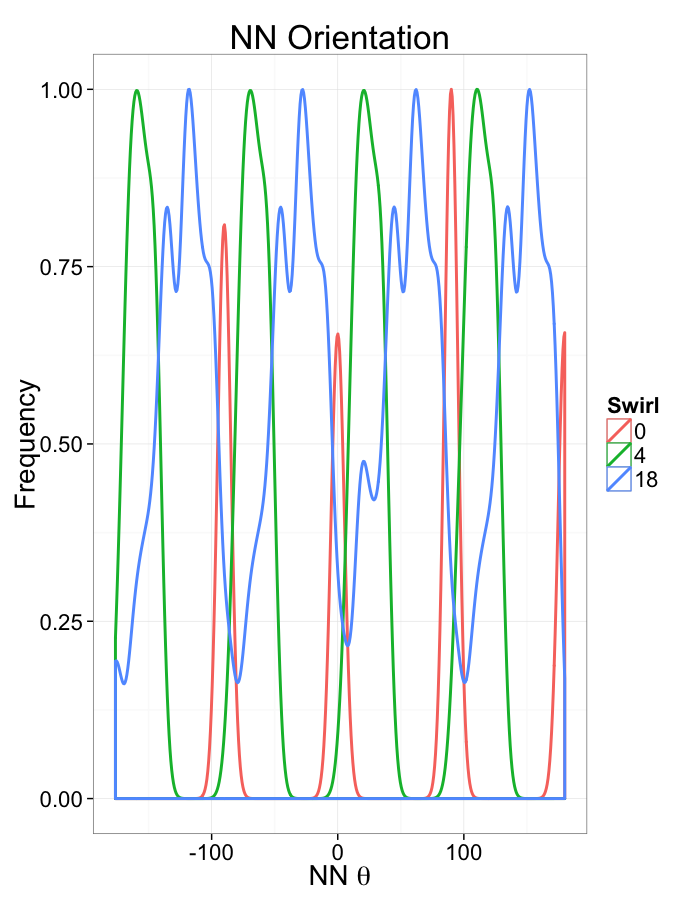
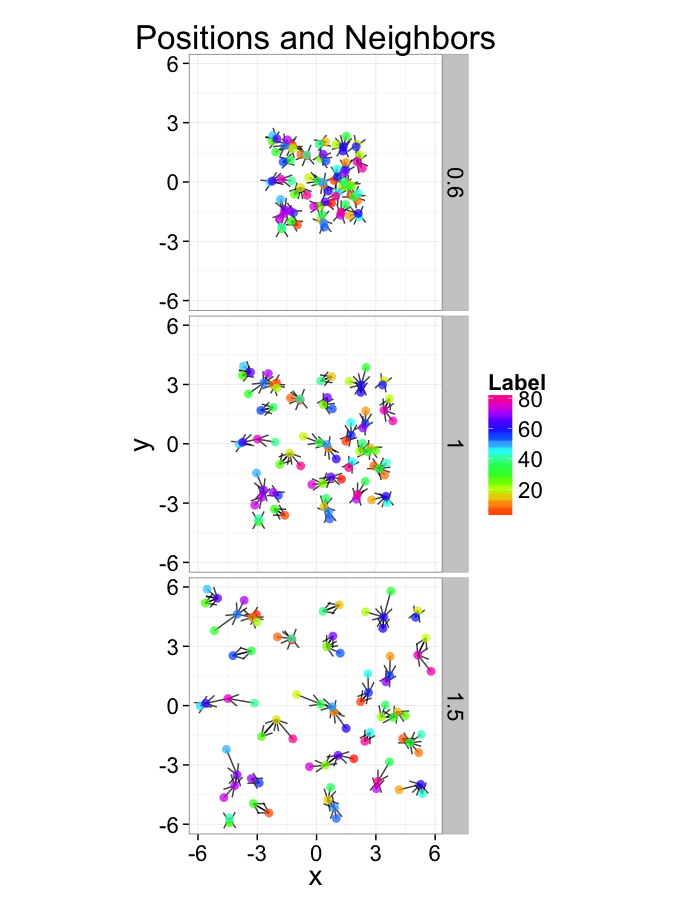
- Swirl
- A transformation where the points are rotated more based on how far away they are from the center and the slope of the swirl (α),
θ(x,y)=α√x2+y2
[x′y′]=[cosθ(x,y)−sinθ(x,y)sinθ(x,y)cosθ(x,y)][xy]
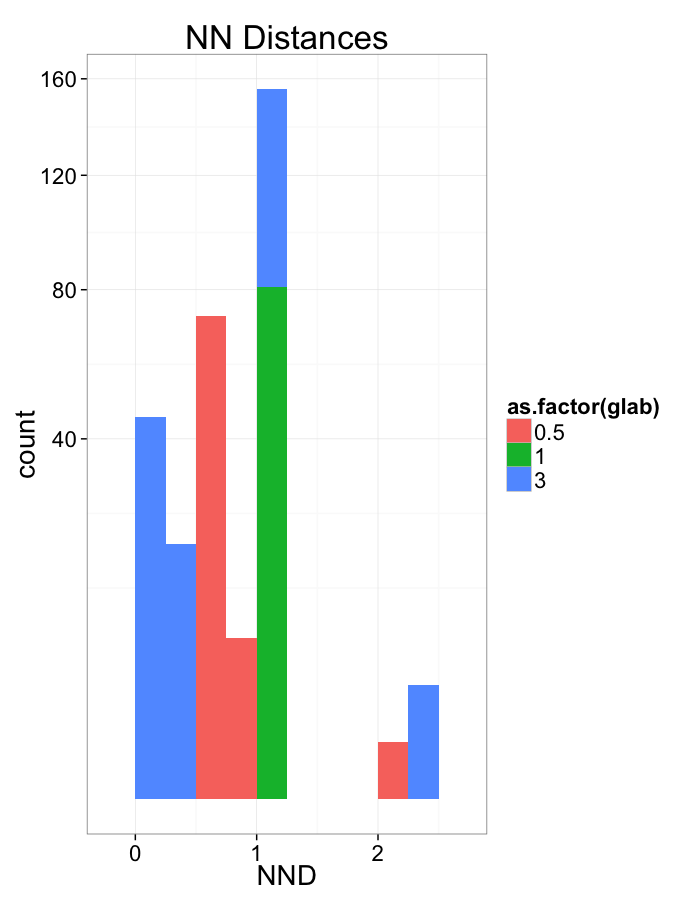
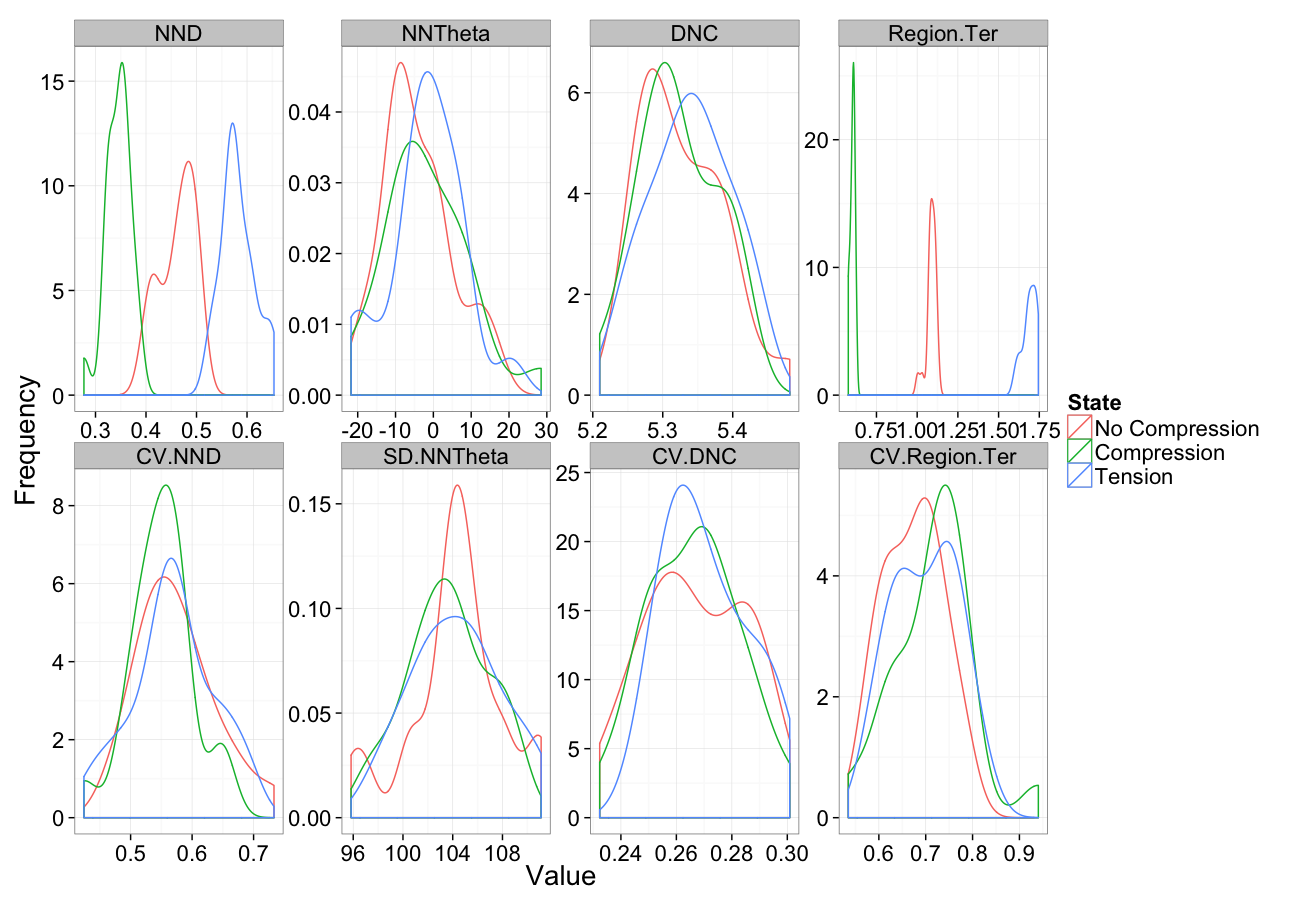
Examining Compression
Compression Distributions
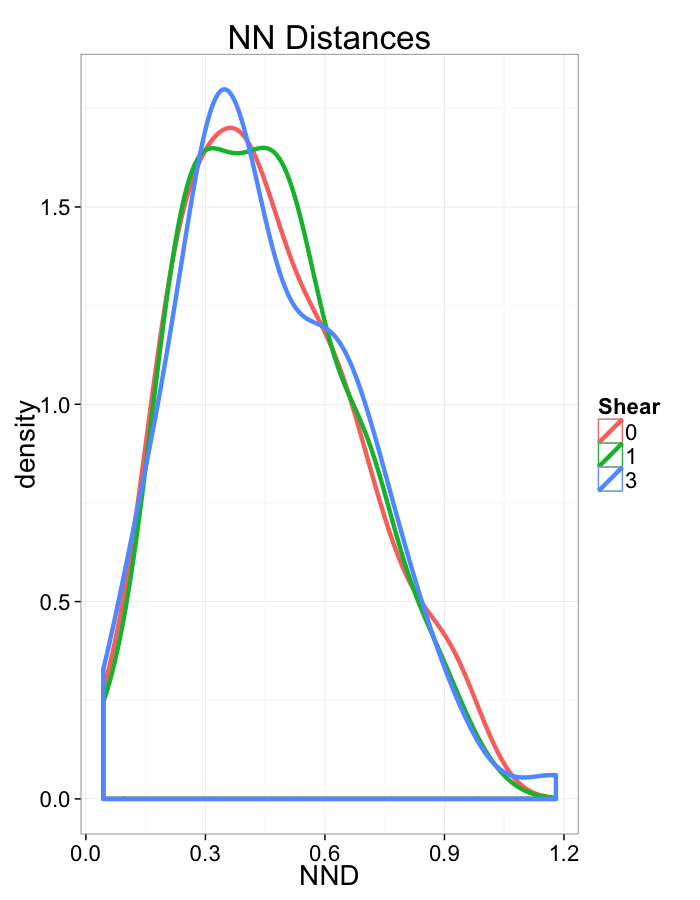
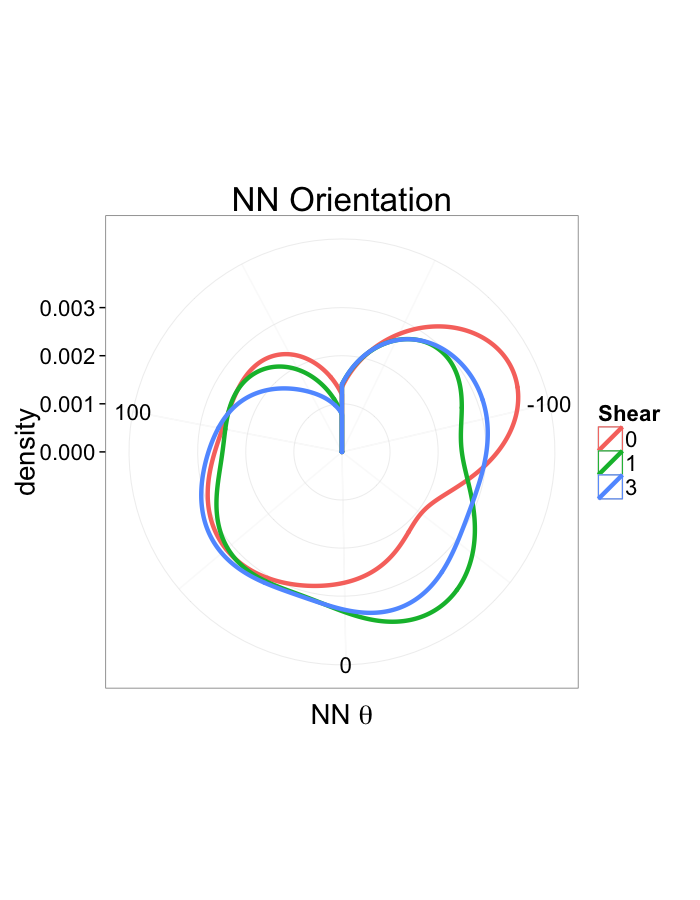
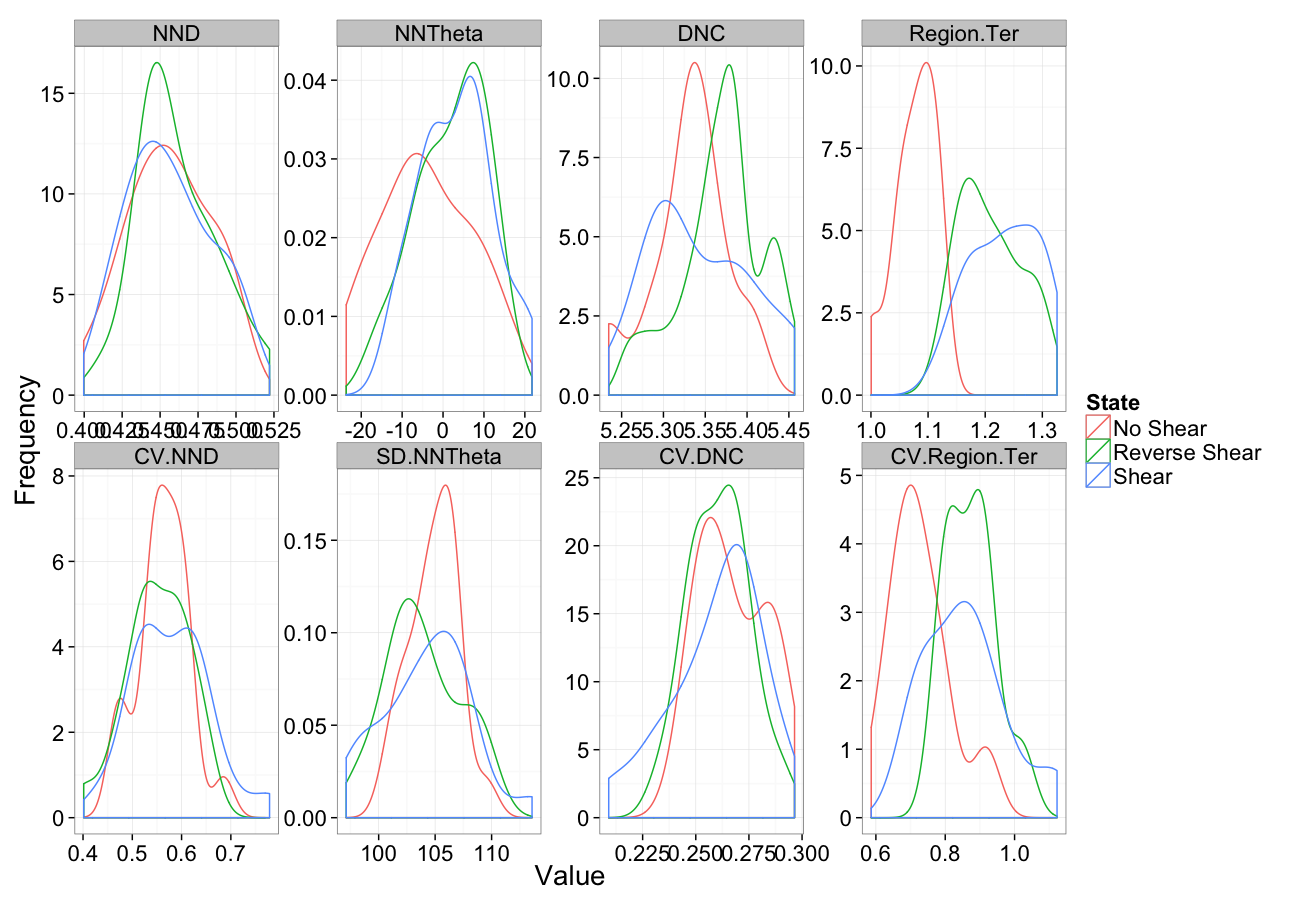
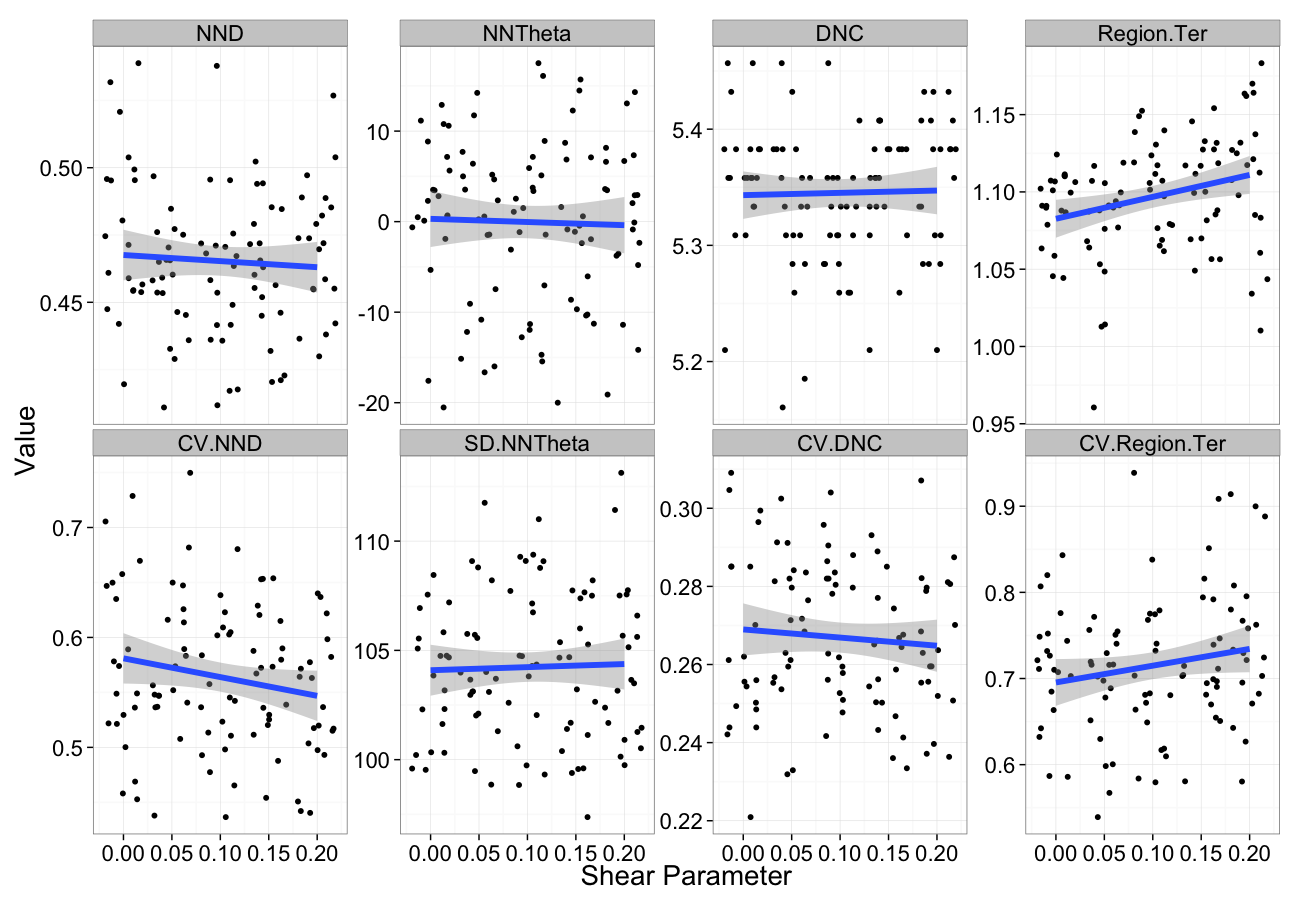
Examining Different Shears
Shear Distributions
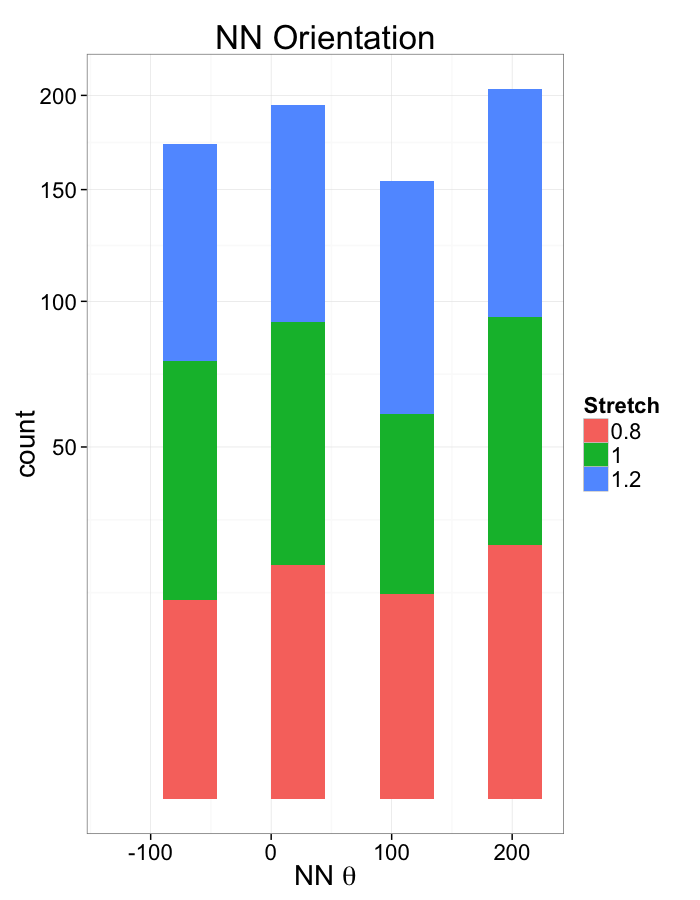
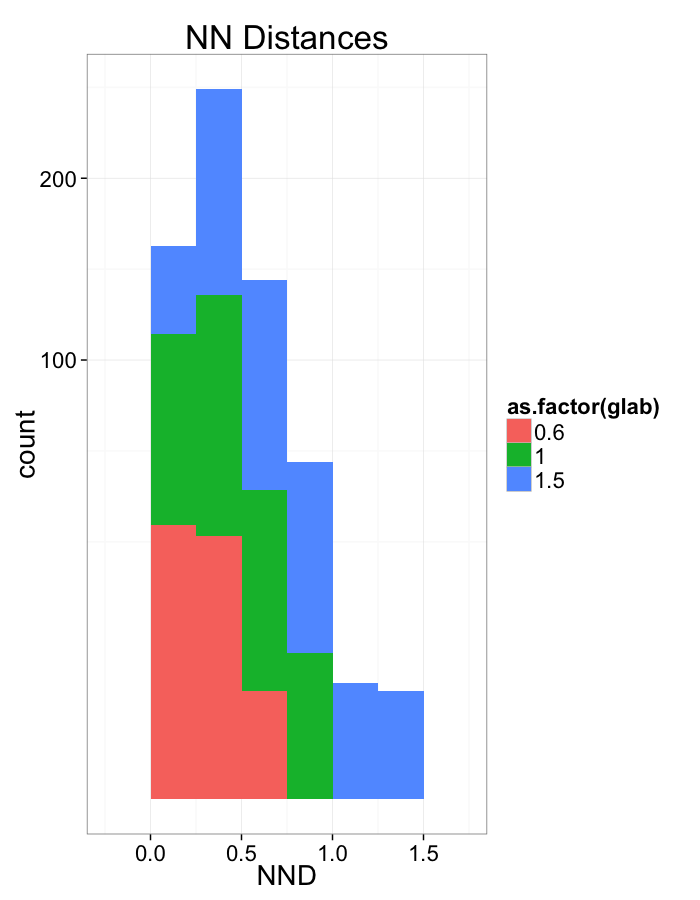
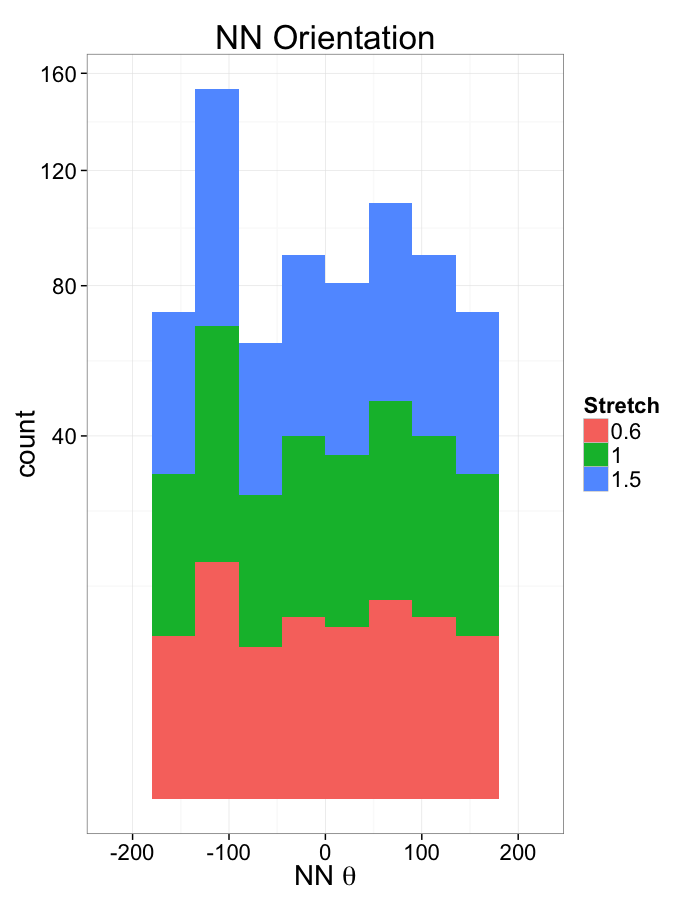
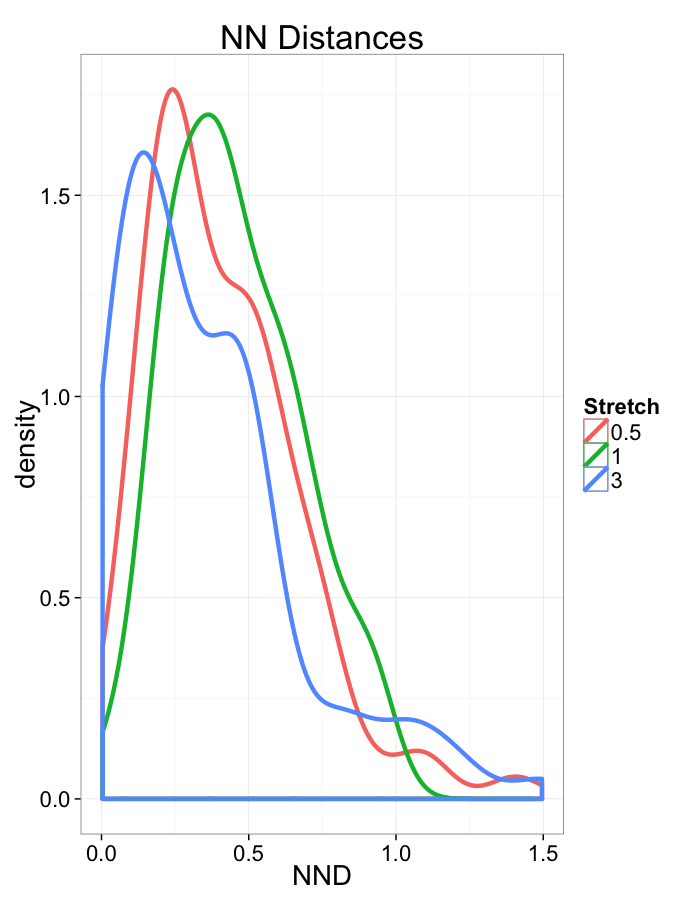
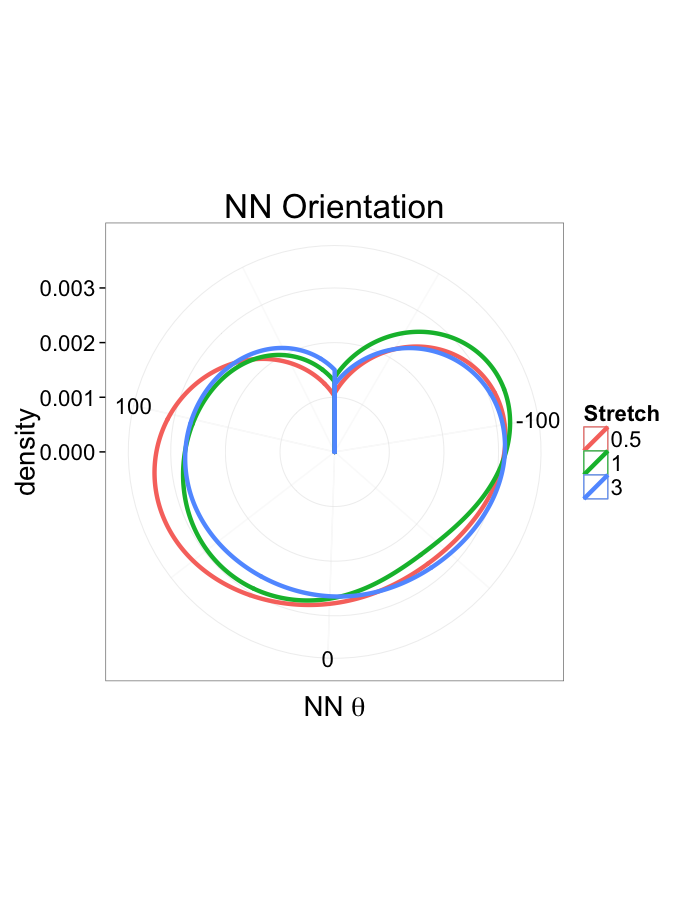
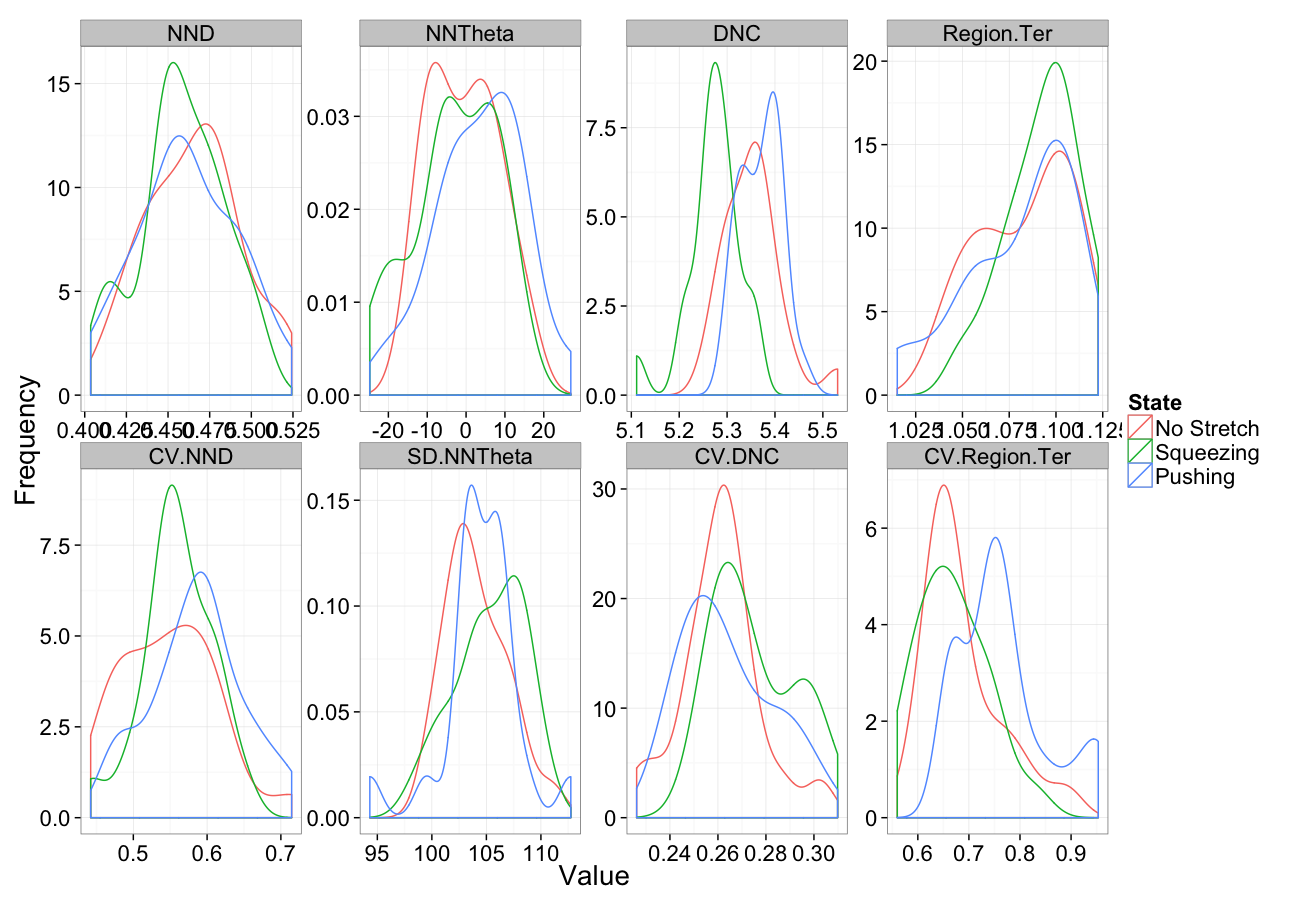
Examining Different Stretches
Stretch Distributions
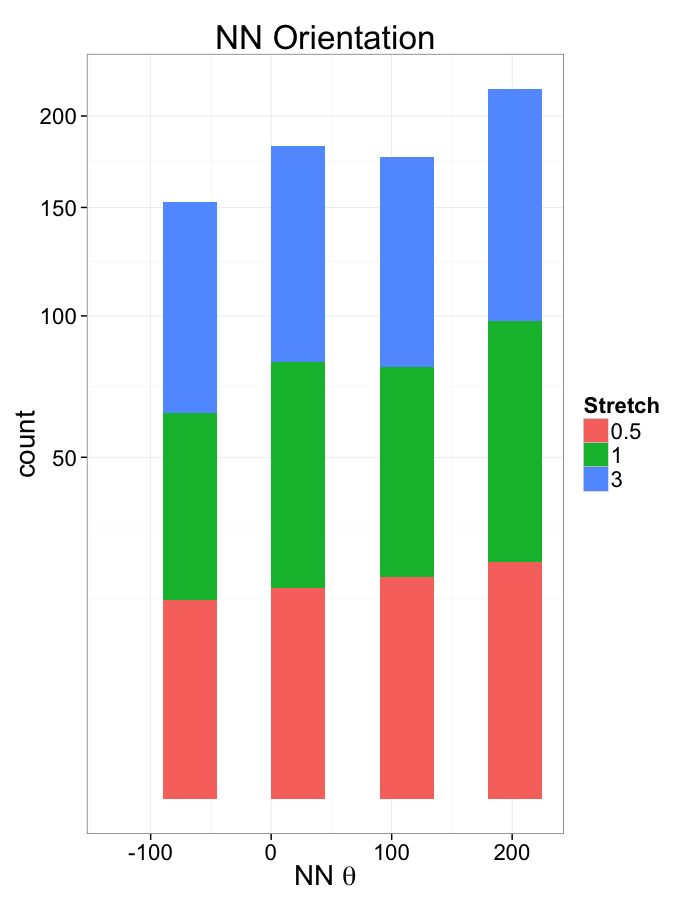
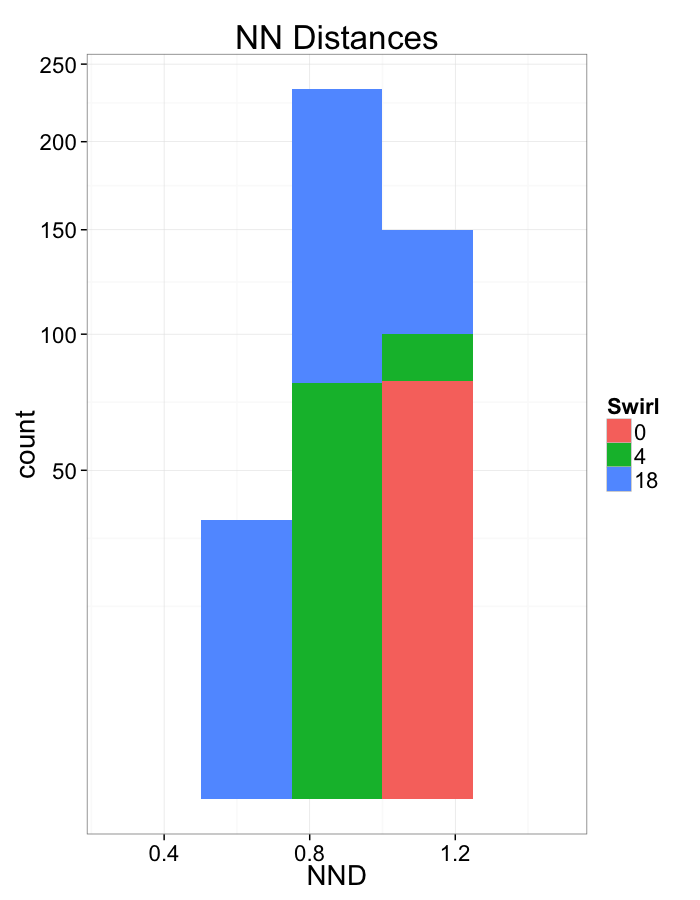
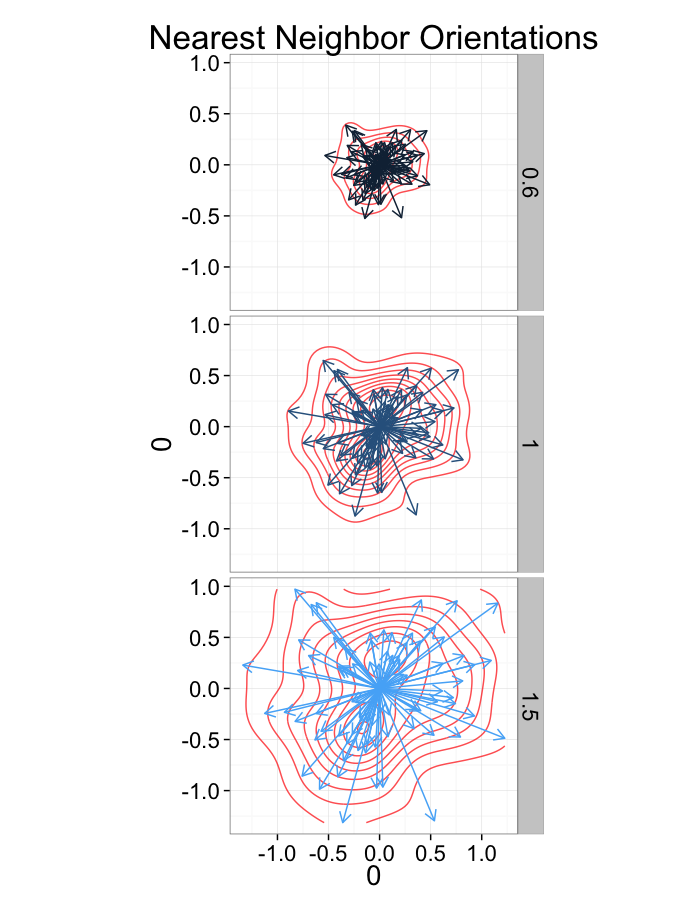
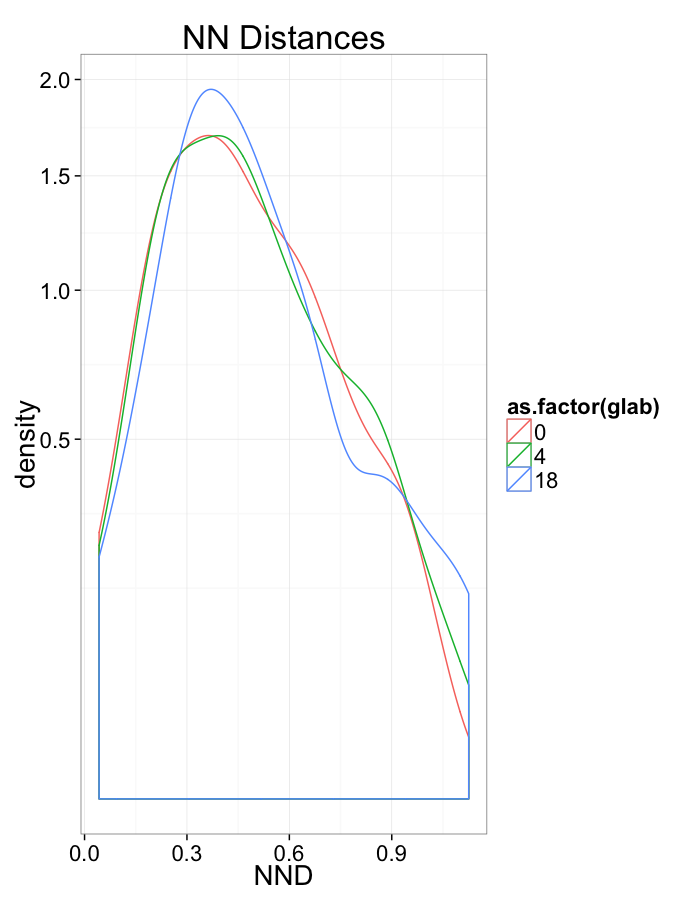
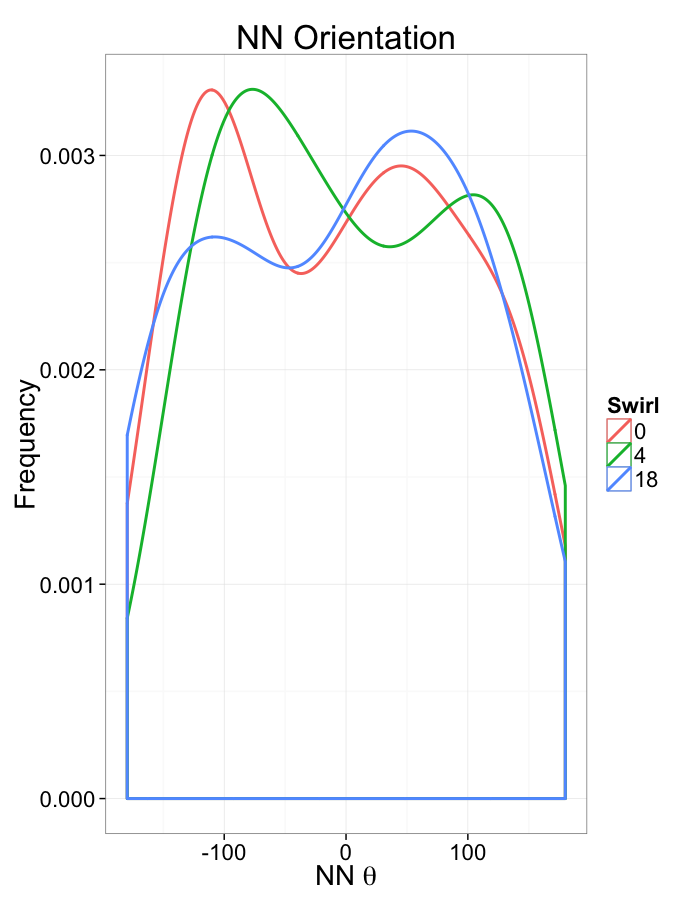
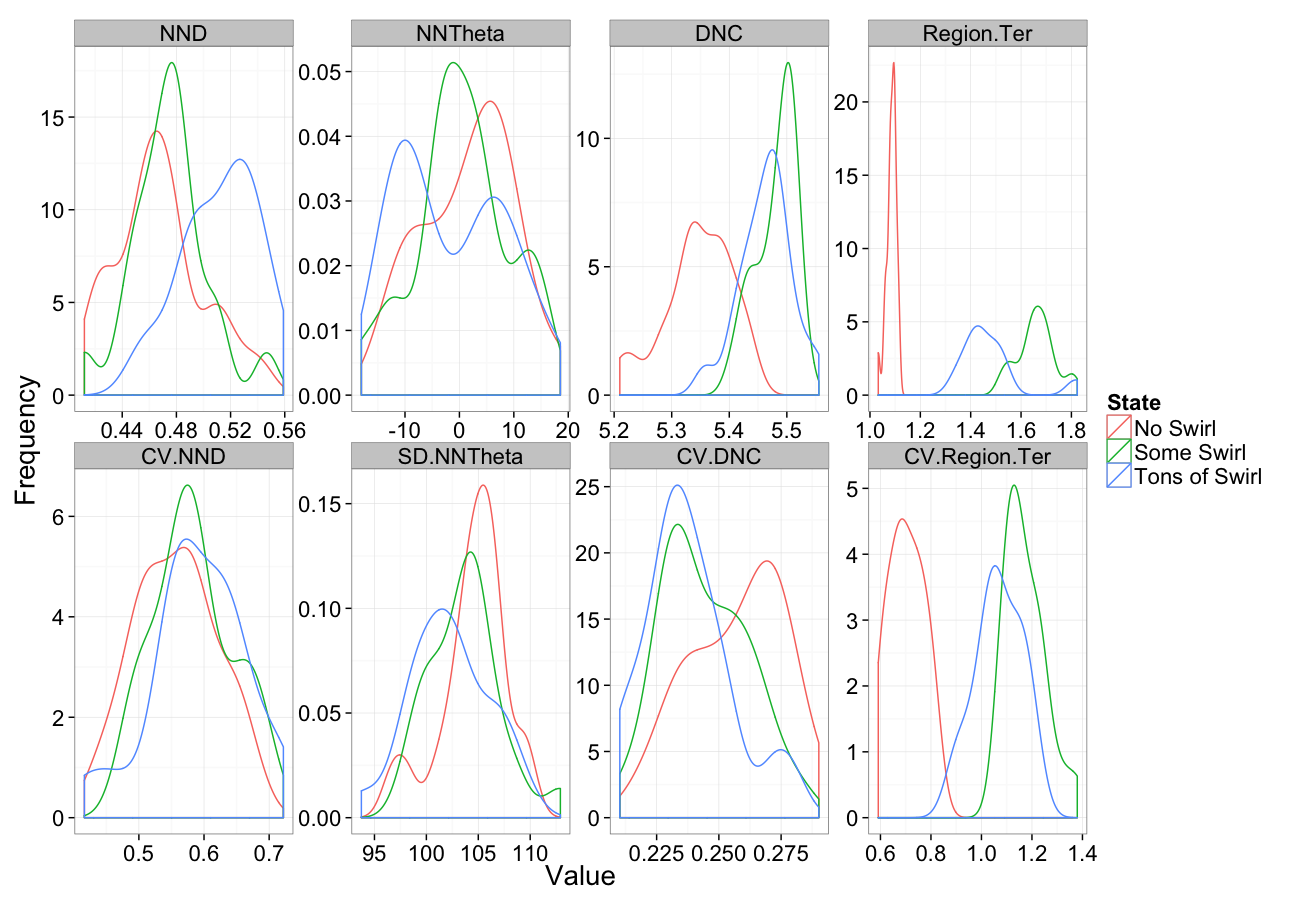
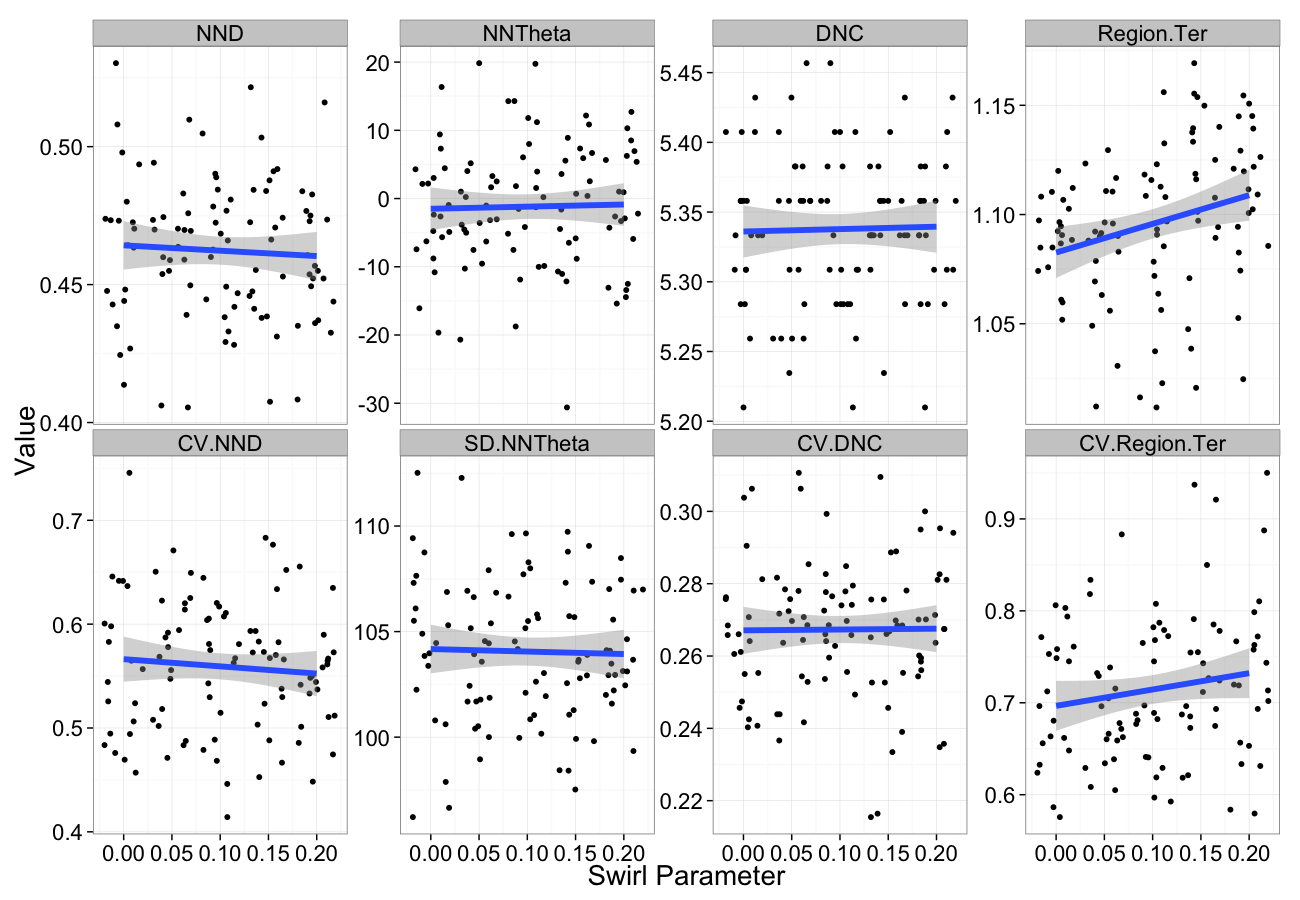
Examining Swirl Systems
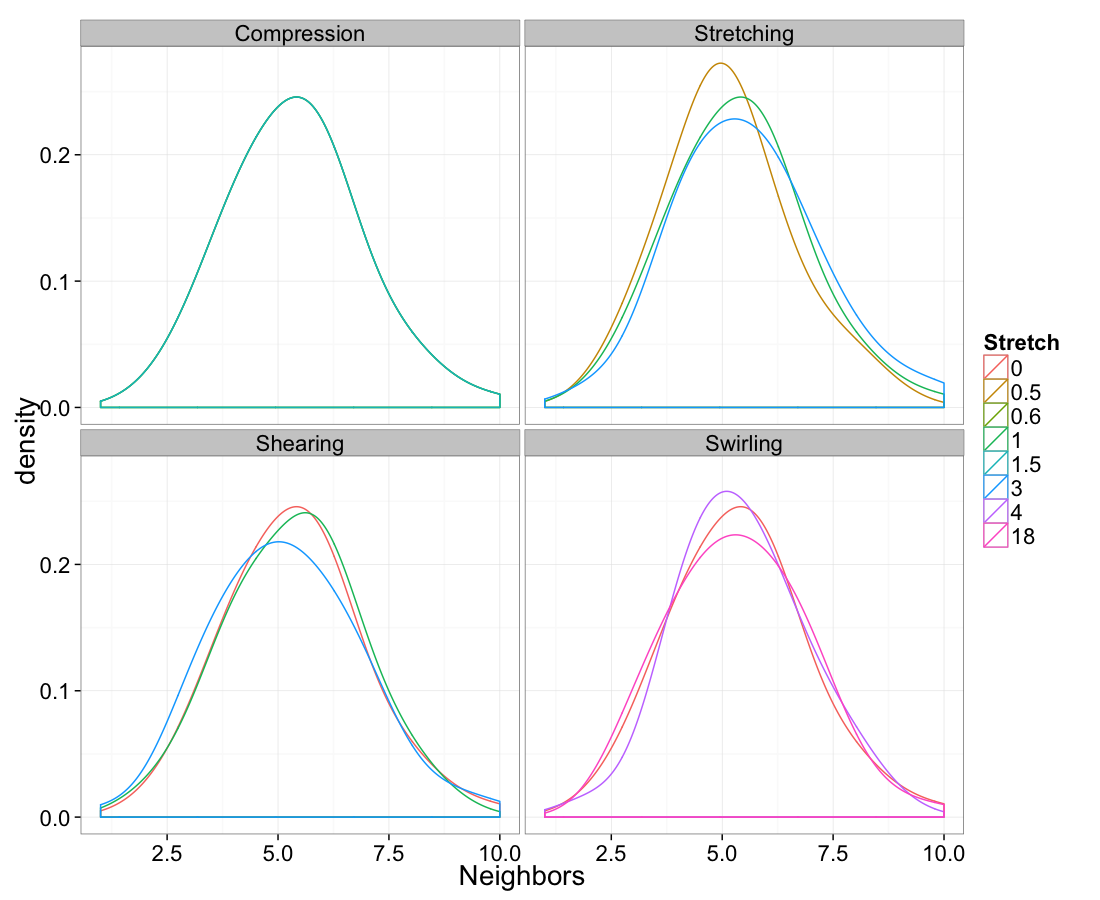
Swirl NN Distributions
What we notice
We notice there are several fairly significant short-comings of these metrics (particularly with in-silico systems)
- Orientation appears to be useful but random
- Why should it matter if one side is 0.01% closer?
- Single outlier objects skew results
- We only extract one piece of information
- Difficult to create metrics
- Fit a peak to the angle distribution and measure the width as the "angle variability"?
Luckily we are not the first people to address this issue
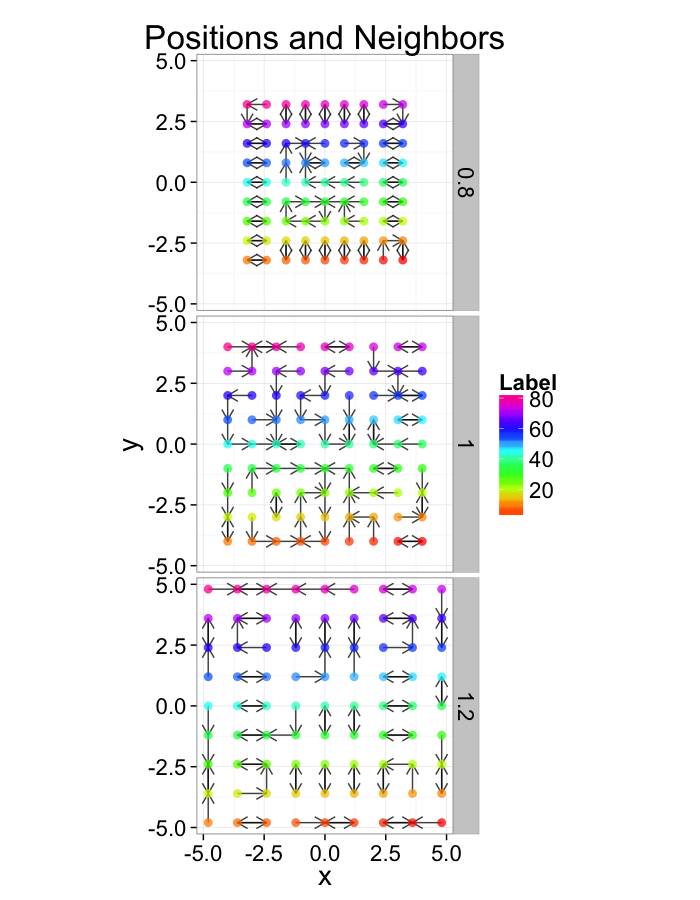
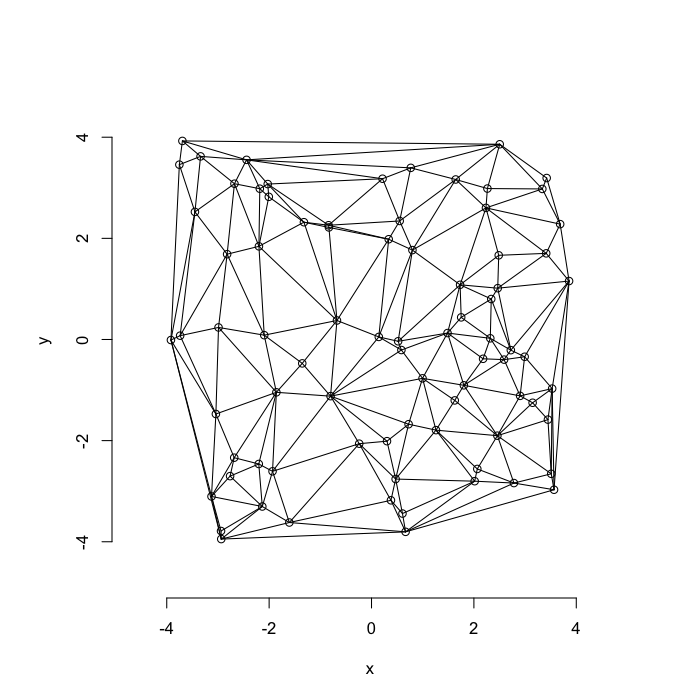
Random Systems
Using a uniform grid of points as a starting point has a strong influence on the results. A better approach is to use a randomly distributed series of points
- resembles real data much better
- avoids these symmetry problems
- ϵ sized edges or overlaps
- identical distances to nearby objects
+/- r Code
Examining Compression
Compression Distributions
Examining Different Shears
Shear Distributions
Examining Different Stretches
Stretch Distributions
Examining Swirl Systems
Swirl NN Distributions
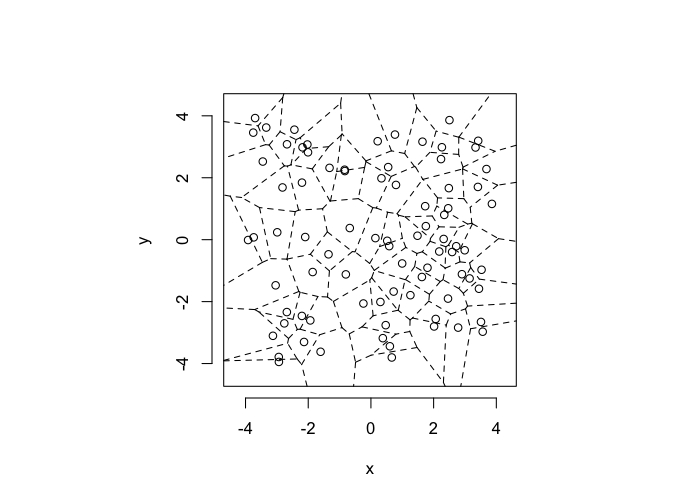
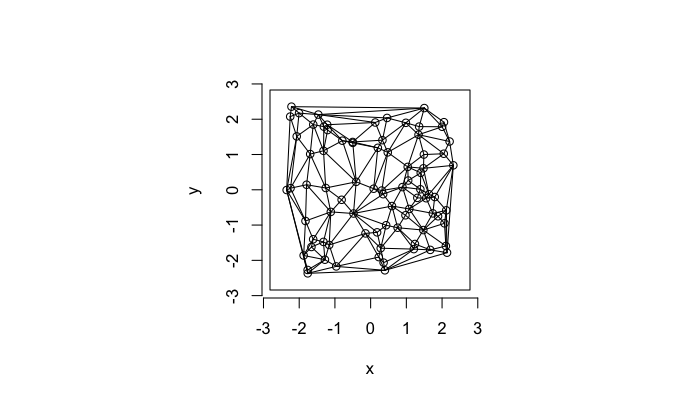
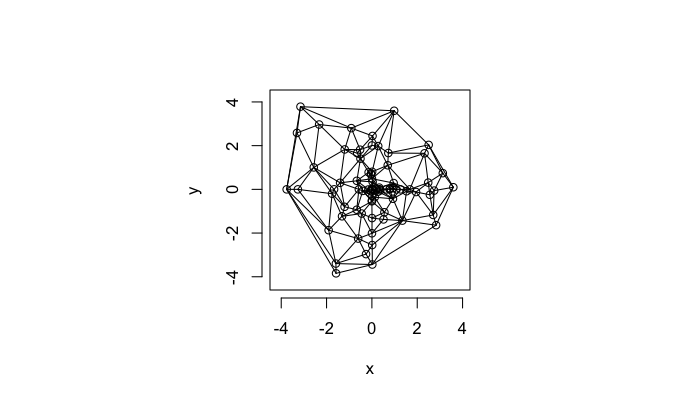
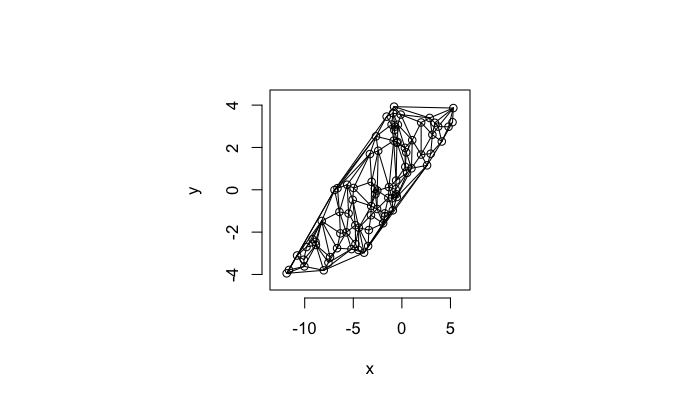
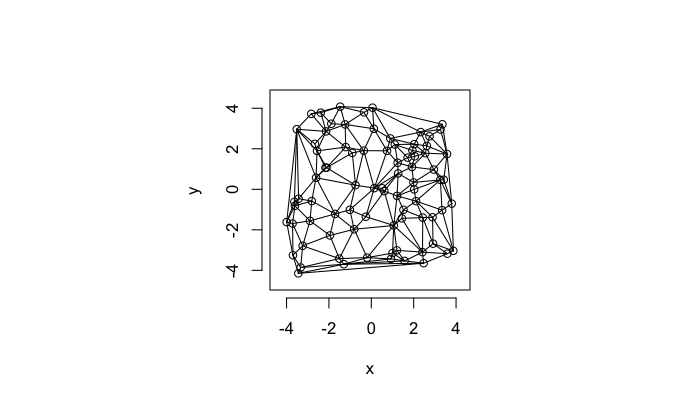
Voronoi Tesselation
+/- r Code
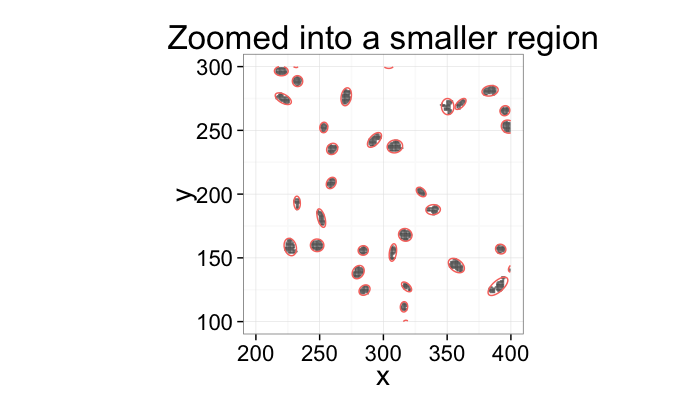
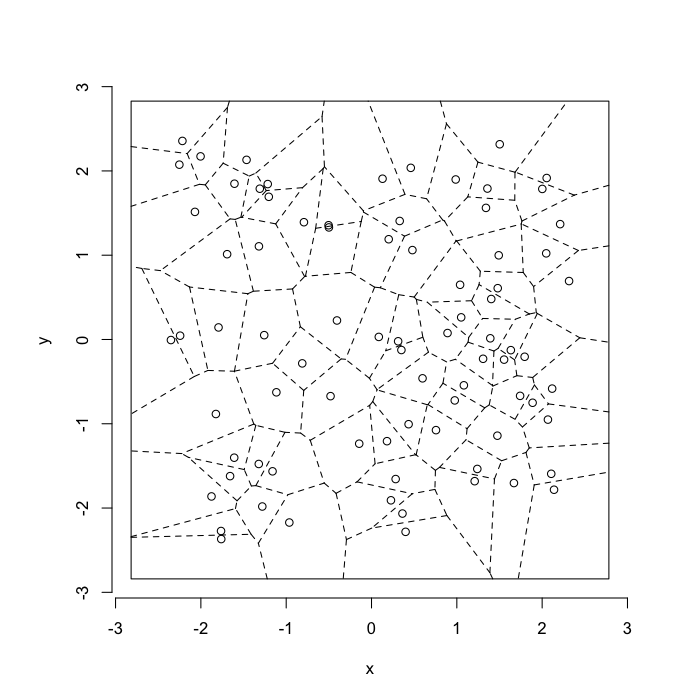
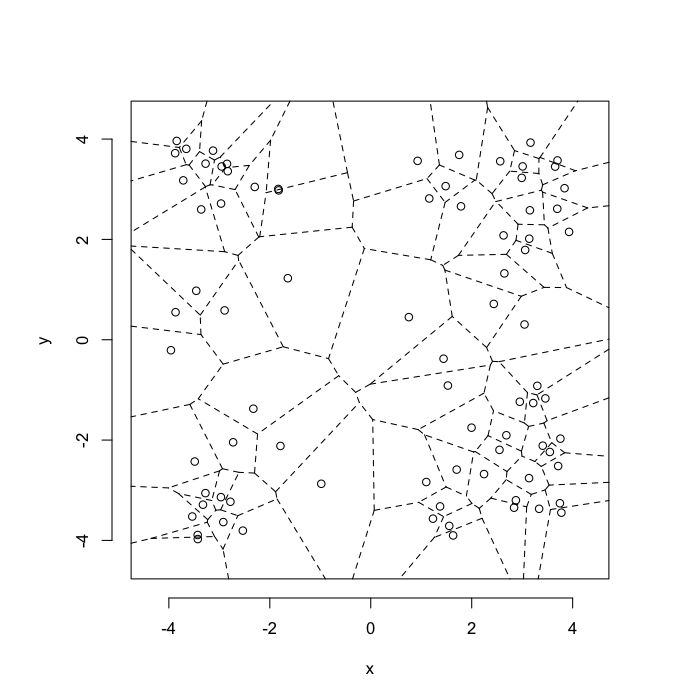
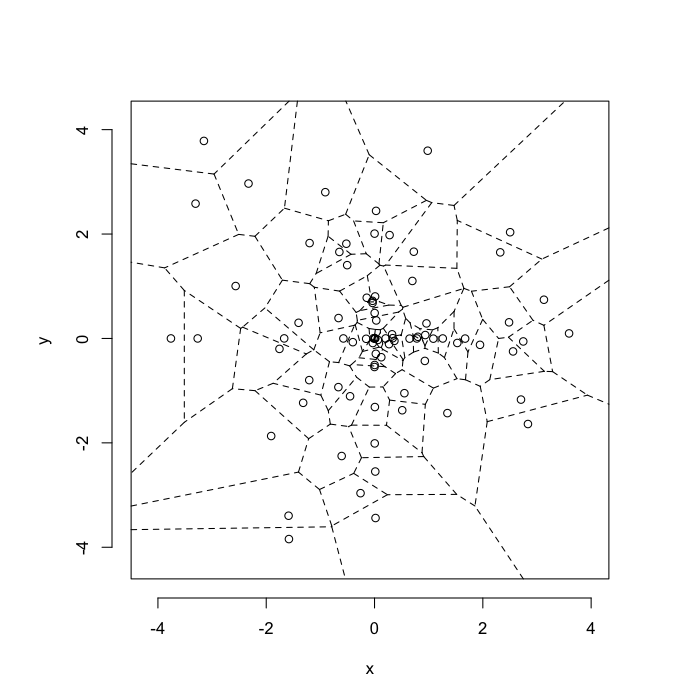
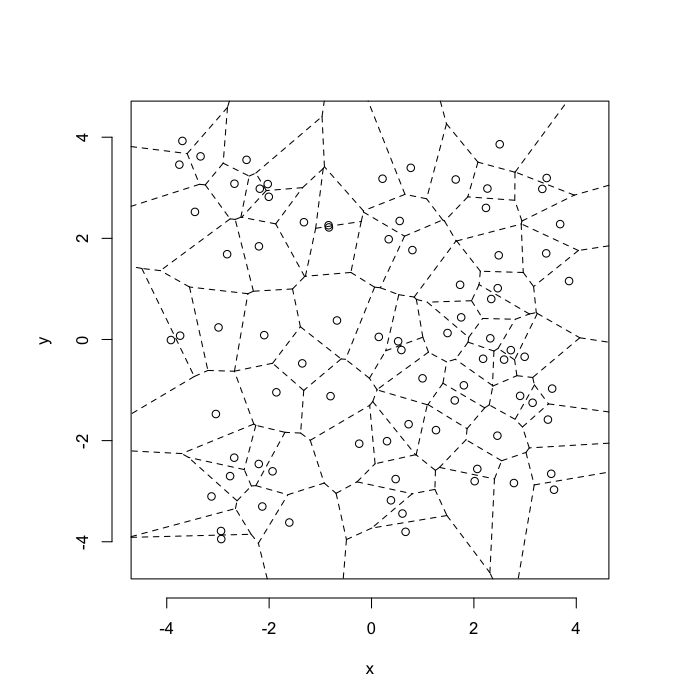
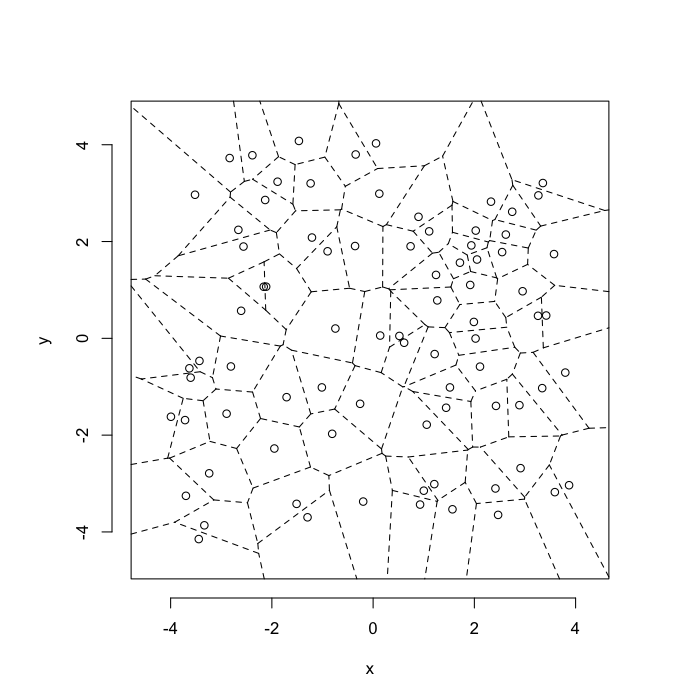
Voronoi tesselation is a method for partitioning a space based on points. The basic idea is that each point →p is assigned a region R consisting of points which are closer to →p than any of the other points. Below the diagram is shown in a dashed line for the points shown as small circles.
We call the area of a region (R) around point →p its territory.
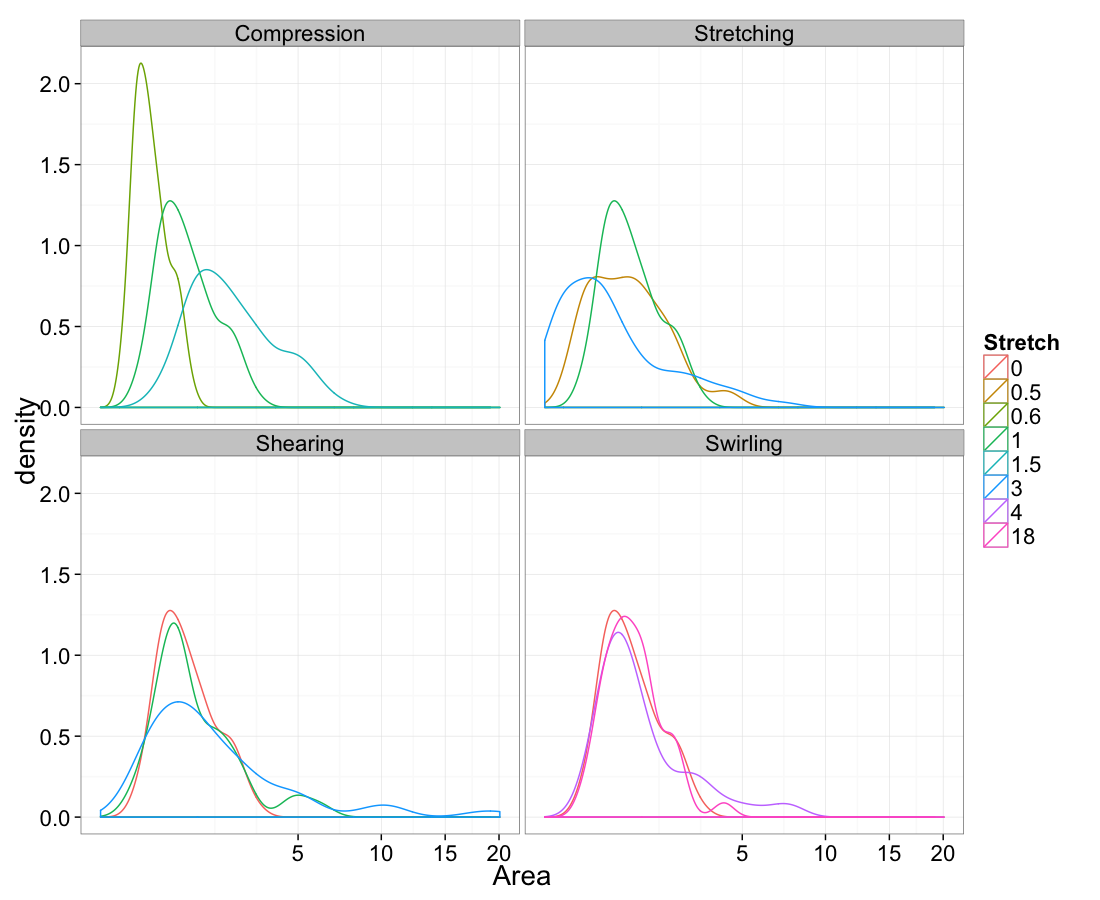
The grid on the random system, shows much more diversity in territory area.
Calculating Density
Back to our original density problem of having just one number to broadly describe the system.
- Can a voronoi tesselation help us with this?
- YES
With density we calculated
Density=Number of ObjectsTotal Volume
with the regions we have a territory (volume) per object so the average territory is
¯Territory=∑TerritoryiNumber of Objects=Total VolumeNumber of Objects=1Density
So the same, but we now have a density definition for a single point!
Densityi=1Territoryi
Density Examples
Delaunay Triangulation
A parallel or dual idea where triangles are used and each triangle is created such that the circle which encloses it contains no other points. The triangulation makes the neighbors explicit since connected points in the triangulation correspond to points in our tesselation which share an edge (or face in 3D)
We define the number of connections each point →p has the Neighbor Count or Delaunay Neighbor Count.
The triangulation on a random system has a much higher diversity in neighbor count
Compression System
Compression
Tension
Shear System
Low Shear
High Shear
Stretch System
Low Stretch
Highly Stretched System
Swirl System
Low Swirl System
High Swirl System
Neighborhoods
Compression
Stretch
Shear
Swirl
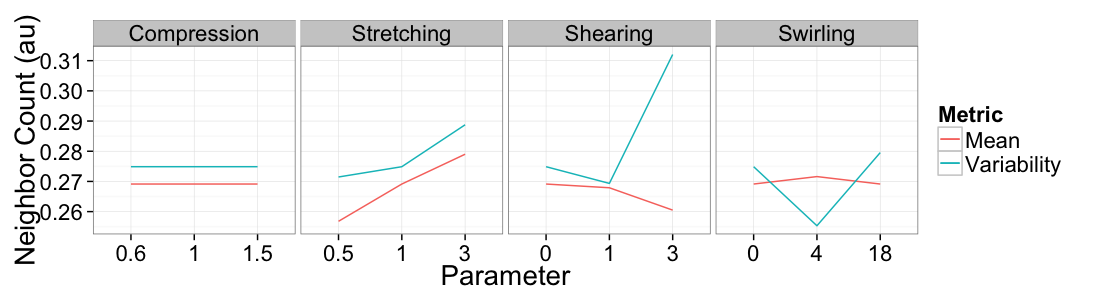
Neighbor Count
+/- r Code
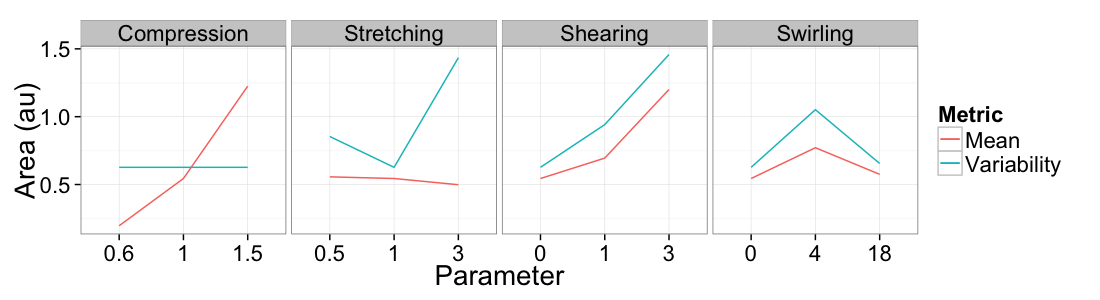
Volume
Mean vs Variability
Where are we at?
We have introduced a number of "operations" we can perform on our objects to change their positions
- compression
- stretching
- shearing
- swirling
We have introduced a number of metrics to characterize our images
- Nearest Neighbor distance
- Nearest Neighbor angle
- Delaunay Neighbor count
- Territory Area (Volume)
A single random systems is useful
- but in order to have a reasonable understanding of the behavior of a system we need to sample many of them.
Understand metrics as a random system + a known transformation
- We take mean values
- Also coefficient of variation (CV) values since they are "scale-free"
+/- r Code
Understanding Metrics
In imaging science we always end up with lots of data, the tricky part is understanding the results that come out. With this simulation-based approach
- we generate completely random data
- apply a known transformation to it F
- quantify the results
We can then take this knowledge and use it to interpret observed data as transformations on an initially random system. We try and find the rules used to produce the sample
Examples
Cell distribution in bone
- Cell position appears random
- Metrics ≠ Random Statistics
- Cells are consistently self-avoiding or stretched
Egg-shell Pores
- Pores in rock / egg shell appear random
- Metrics ≠ Random Statistics
- Pores are also self-avoiding
Compression
Compression Sensitivity
Stretching
Stretching Sensitivity
Shearing
Shearing Sensitivity
Swirling
Swirling Sensitivity
Self-Avoiding
From the nearest neighbor distance metric, we can create a scale-free version of the metric which we call self-avoiding coefficient or grouping.
The metric is the ratio of
- observed nearest neighbor distance NND
- the expected mean nearest neighbor distance (r0) for a random point distribution (Poisson Point Process) with the same number of points (N.Obj) per volume (Total.Volume). r0=3√Total.Volume2π N.Obj
Using the territory we defined earlier (Region area/volume) we can simplify the definition to
r0=3√¯Ter2π
SAC=NND3√¯Ter2π
Distribution Tensor
So the information we have is 3D why are we taking single metrics (distance, angle, volume) to quantify it.
- Shouldn't we use 3D metrics with 3D data?
- Just like the shape tensor we covered before, we can define a distribution tensor to characterize the shape of the distribution.
- The major difference instead of constituting voxels we use edges
- an edge is defined from the Delaunay triangluation
- it connects two neighboring bubbles together
- We can calculate distribution for a single bubble by taking all edges that touch the object or from a region by finding all edges inside that region
We start off by calculating the covariance matrix from the list of edges →vij in a given volume V
→vij=→COV(i)−→COV(j)
COV(V)=1N∑∀COM(i)∈V[→vx→vx→vx→vy→vx→vz→vy→vx→vy→vy→vy→vz→vz→vx→vz→vy→vz→vz]
Distribution Tensor (continued)
We then take the eigentransform of this array to obtain the eigenvectors (principal components, →Λ1⋯3) and eigenvalues (scores, λ1⋯3)
COV(Iid)⟶[→Λ1x→Λ1y→Λ1z→Λ2x→Λ2y→Λ2z→Λ3x→Λ3y→Λ3z]⏟Eigenvectors∗[λ1000λ2000λ3]⏟Eigenvalues∗[→Λ1x→Λ1y→Λ1z→Λ2x→Λ2y→Λ2z→Λ3x→Λ3y→Λ3z]T⏟Eigenvectors The principal components tell us about the orientation of the object and the scores tell us about the corresponding magnitude (or length) in that direction.
Distribution Anisotropy
Visual example
- Tensor represents the average spacing between objects in each direction ≈ thickness of background.
- Its interpretation is more difficult since it doesn't represent a real object

From this tensor we can define an anisotropy in the same manner as we defined for shapes. The anisotropy defined as before Aiso=Longest Side−Shortest SideLongest Side
- An isotropic distribution tensor indicates the spacing between objects is approximately the same in every direction
- Does not mean a grid, organized, or evenly spaced!
- Just the same in every direction
- Anisotropic distribution tensor means the spacing is smaller in one direction than the others
- Can be regular or grid-like
- Just closer on one direction
Distribution Oblateness

From this tensor we can also define oblateness in the same manner as we defined for shapes. The oblateness is also defined as before as a type of anisotropy
Ob=2λ2−λ1λ3−λ1−1
- Indicates the pancakeness of the distribution
- Oblate means it is very closely spaced in one direction and far in the other two
- strand-like structure
- Prolate means it is close in two directions and far in the other
- sheet-like structure
Orientation
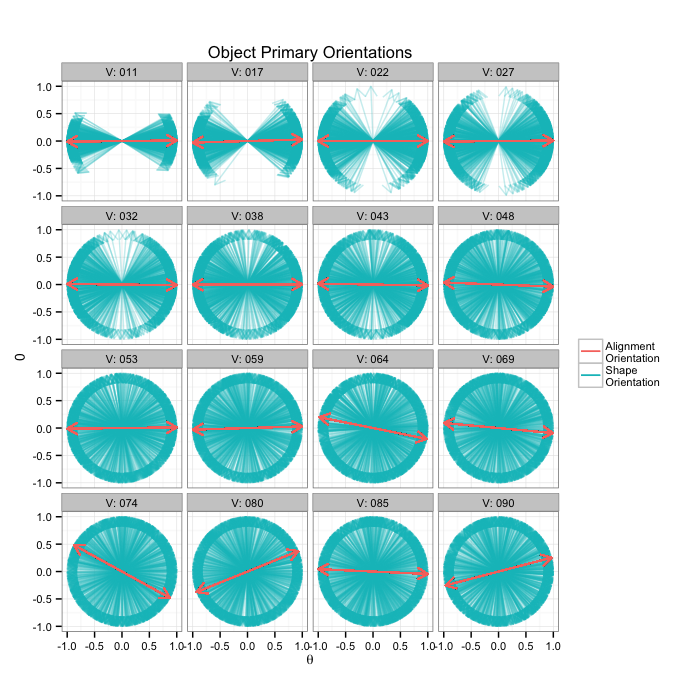
The shape tensor provides for each object 3 possible orientations (each of the eigenvectors). For simplicity we will take the primary direction (but the others can be taken as well, and particularly in oblate or pancake shaped objects the first is probably not the best choice!)
Orientation
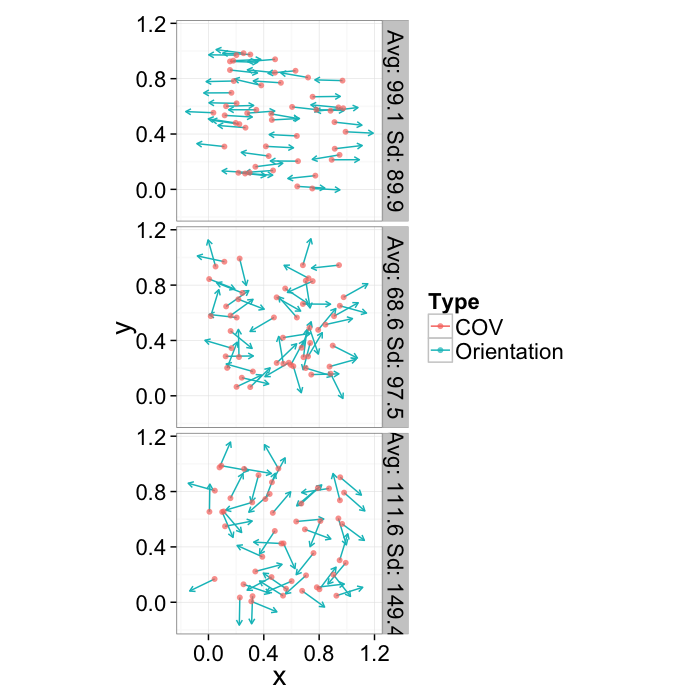
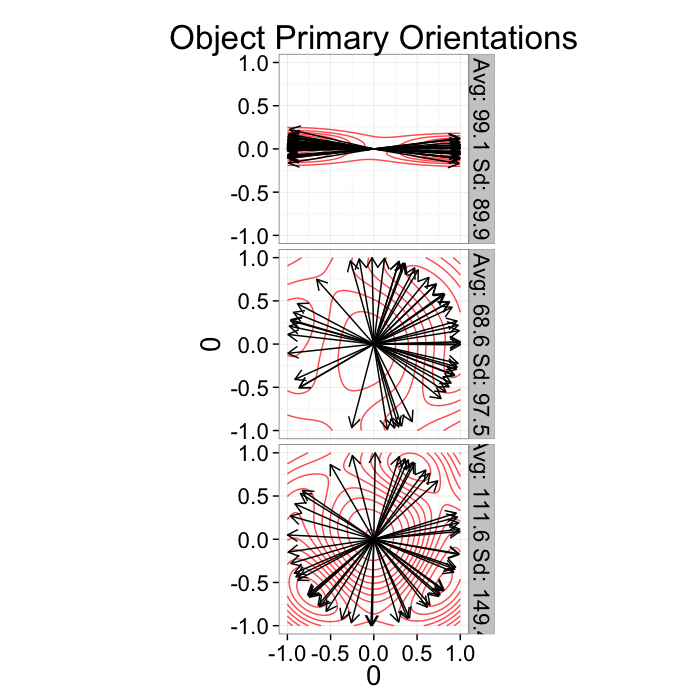
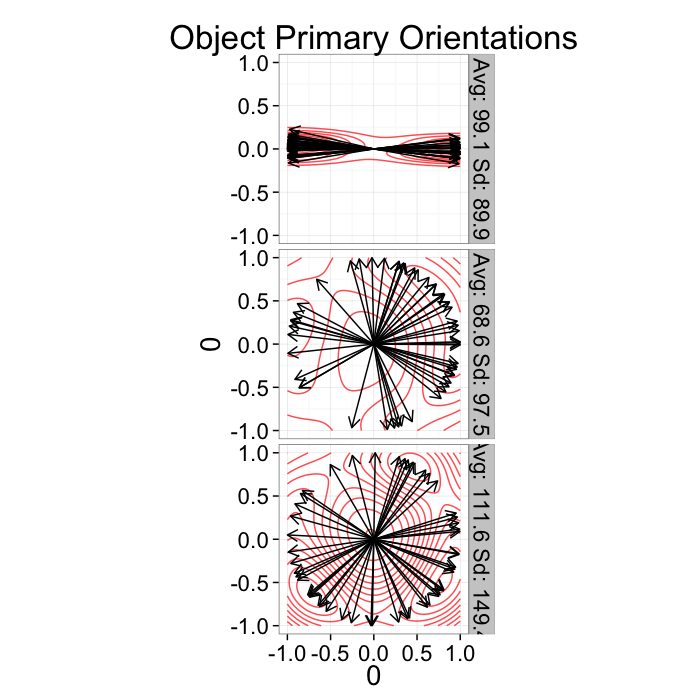
Since orientation derived from a shape tensor / ellipsoid model has no heads or tails. The orientation is only down to a sign ⟶==⟵ and ↑==↓.
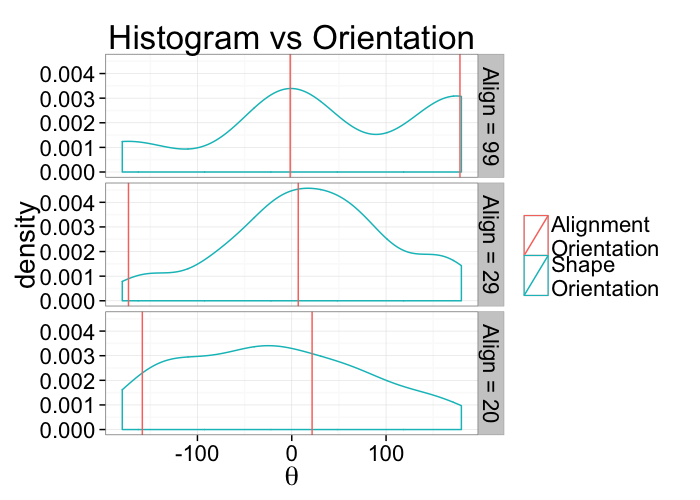
This means calculating the average and standard deviation are very poor desciptors of the actual dataset. The average for all samples below is around 90 (vertical) even though almost no samples are vertical and the first sample shows a very high (90) standard deviation even though all the samples in reality have the same orientation.
+/- r Code
| Angle.Variability | Mean.Angle | Sd.Angle |
|---|---|---|
| 5.729578 | 99.14070 | 89.91135 |
| 62.864789 | 68.63894 | 97.47078 |
| 120.000000 | 111.58325 | 149.44605 |
The problem can be dealt with by using the covariance matrix which takes advantage of the products which makes the final answer independent of sign.
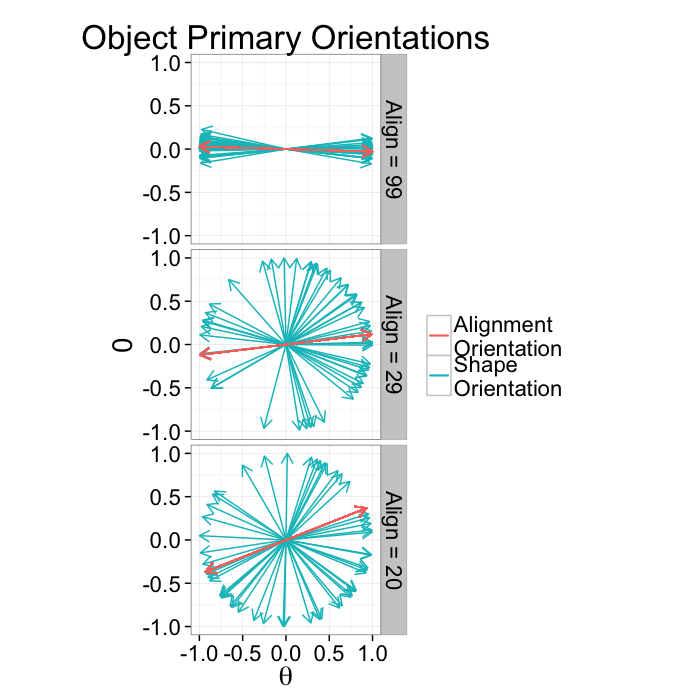
Alignment Tensor
We can again take advantage of the versatility of a tensor representation for our data and use an alignment tensor.
- The same as all of the tensors we have introduced
- Except we use the primary orientation instead of voxel positions (shape) or edges (distribution)
- Similar to distribution it is calculated for a volume (V) or region and is meaningless for a single object
→vi=→Λ1(i)
COV=1N∑∀COM(i)∈V[→vx→vx→vx→vy→vx→vz→vy→vx→vy→vy→vy→vz→vz→vx→vz→vy→vz→vz]

Alignment Tensor: Example
Using the example from before
Show some tensor stuff here
+/- r Code
Alignment Anisotropy
Anisotropy for alignment can be summarized as degree of alignment since very anisotropic distributions mean the objects are aligned well in the same direction while an isotropic distribution means the orientations are random. Oblateness can also be defined but is normally not particularly useful.
Aiso=Longest Side−Shortest SideLongest Side

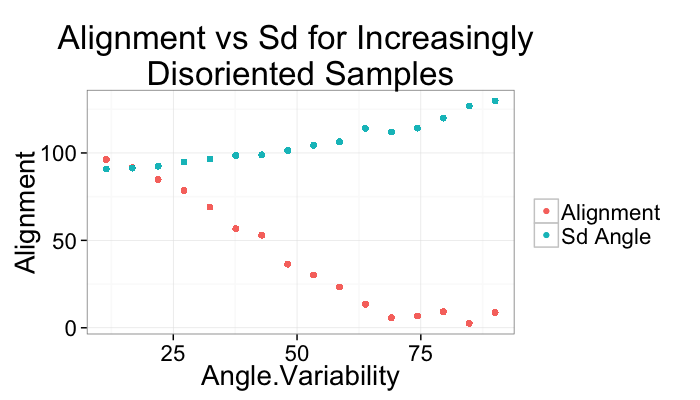
Alignment Anisotropy Applied
+/- r Code
| Angle.Variability | Mean.Angle | Sd.Angle | Alignment |
|---|---|---|---|
| 5.729578 | 99.14070 | 89.91135 | 99.21383 |
| 62.864789 | 68.63894 | 97.47078 | 28.88033 |
| 120.000000 | 111.58325 | 149.44605 | 19.56784 |
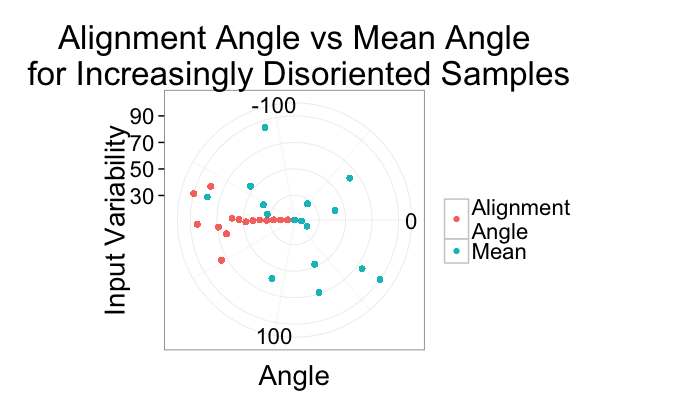
Alignment for many samples
Angle Accuracy
Variability Accuracy
Other Approaches
K-Means
K-Means can also be used to classify the point-space itself after shape analysis. It is even better suited than for images because while most images are only 2 or 3D the shape vector space can be 50-60 dimensional and is inherently much more difficult to visualize.
2 Point Correlation Functions
For a wider class of analysis of spatial distribution, there exist a class a functions called N-point Correlation Functions
- given a point of type A at →x
what is the probability of B at →x+→r
How is it useful
- A simple analysis can be used to see the spacing of objects (peaks in the F(→r) function, A and B are the same phase).
- Where are cells located in reference to canals (peaks in F(→r) function, A is a point inside a canal B is the cells)