## Loading required package: knitr

## The basic files and libraries needed for most presentations
# creates the libraries and common-functions sections
read_chunk("../common/utility_functions.R")

require(ggplot2) #for plots
require(lattice) # nicer scatter plots
require(plyr) # for processing data.frames
library(dplyr)
require(grid) # contains the arrow function
require(jpeg)
require(doMC) # for parallel code
require(png) # for reading png images
require(gridExtra)

require(reshape2) # for the melt function
#if (!require("biOps")) {
#  # for basic image processing
#  devtools::install_github("cran/biOps")
#  library("biOps")
#}
## To install EBImage
if (!require("EBImage")) { # for more image processing
  source("http://bioconductor.org/biocLite.R")
  biocLite("EBImage")
}

used.libraries<-c("ggplot2","lattice","plyr","reshape2","grid","gridExtra","biOps","png","EBImage")

# start parallel environment
registerDoMC()
# functions for converting images back and forth
im.to.df<-function(in.img,out.col="val") {
  out.im<-expand.grid(x=1:nrow(in.img),y=1:ncol(in.img))
  out.im[,out.col]<-as.vector(in.img)
  out.im
}
df.to.im<-function(in.df,val.col="val",inv=F) {
  in.vals<-in.df[[val.col]]
  if(class(in.vals[1])=="logical") in.vals<-as.integer(in.vals*255)
  if(inv) in.vals<-255-in.vals
  out.mat<-matrix(in.vals,nrow=length(unique(in.df$x)),byrow=F)
  attr(out.mat,"type")<-"grey"
  out.mat
}
ddply.cutcols<-function(...,cols=1) {
  # run standard ddply command 
  cur.table<-ddply(...)
  cutlabel.fixer<-function(oVal) {
    sapply(oVal,function(x) {
      cnv<-as.character(x)
      mean(as.numeric(strsplit(substr(cnv,2,nchar(cnv)-1),",")[[1]]))
    })
  }
  cutname.fixer<-function(c.str) {
    s.str<-strsplit(c.str,"(",fixed=T)[[1]]
    t.str<-strsplit(paste(s.str[c(2:length(s.str))],collapse="("),",")[[1]]
    paste(t.str[c(1:length(t.str)-1)],collapse=",")
  }
  for(i in c(1:cols)) {
    cur.table[,i]<-cutlabel.fixer(cur.table[,i])
    names(cur.table)[i]<-cutname.fixer(names(cur.table)[i])
  }
  cur.table
}

# since biOps isn't available use a EBImage based version
imgSobel<-function(img) {
  kern<-makeBrush(3)*(-1)
  kern[2,2]<-8
  filter2(img,kern)
}


show.pngs.as.grid<-function(file.list,title.fun,zoom=1) {
  preparePng<-function(x) rasterGrob(readPNG(x,native=T,info=T),width=unit(zoom,"npc"),interp=F)
  labelPng<-function(x,title="junk") (qplot(1:300, 1:300, geom="blank",xlab=NULL,ylab=NULL,asp=1)+
                                        annotation_custom(preparePng(x))+
                                        labs(title=title)+theme_bw(24)+
                                        theme(axis.text.x = element_blank(),
                                              axis.text.y = element_blank()))
  imgList<-llply(file.list,function(x) labelPng(x,title.fun(x)) )
  do.call(grid.arrange,imgList)
}
## Standard image processing tools which I use for visualizing the examples in the script
commean.fun<-function(in.df) {
  ddply(in.df,.(val), function(c.cell) {
    weight.sum<-sum(c.cell$weight)
    data.frame(xv=mean(c.cell$x),
               yv=mean(c.cell$y),
               xm=with(c.cell,sum(x*weight)/weight.sum),
               ym=with(c.cell,sum(y*weight)/weight.sum)
    )
  })
}

colMeans.df<-function(x,...) as.data.frame(t(colMeans(x,...)))

pca.fun<-function(in.df) {
  ddply(in.df,.(val), function(c.cell) {
    c.cell.cov<-cov(c.cell[,c("x","y")])
    c.cell.eigen<-eigen(c.cell.cov)
    
    c.cell.mean<-colMeans.df(c.cell[,c("x","y")])
    out.df<-cbind(c.cell.mean,
                  data.frame(vx=c.cell.eigen$vectors[1,],
                             vy=c.cell.eigen$vectors[2,],
                             vw=sqrt(c.cell.eigen$values),
                             th.off=atan2(c.cell.eigen$vectors[2,],c.cell.eigen$vectors[1,]))
    )
  })
}
vec.to.ellipse<-function(pca.df) {
  ddply(pca.df,.(val),function(cur.pca) {
    # assume there are two vectors now
    create.ellipse.points(x.off=cur.pca[1,"x"],y.off=cur.pca[1,"y"],
                          b=sqrt(5)*cur.pca[1,"vw"],a=sqrt(5)*cur.pca[2,"vw"],
                          th.off=pi/2-atan2(cur.pca[1,"vy"],cur.pca[1,"vx"]),
                          x.cent=cur.pca[1,"x"],y.cent=cur.pca[1,"y"])
  })
}

# test function for ellipse generation
# ggplot(ldply(seq(-pi,pi,length.out=100),function(th) create.ellipse.points(a=1,b=2,th.off=th,th.val=th)),aes(x=x,y=y))+geom_path()+facet_wrap(~th.val)+coord_equal()
create.ellipse.points<-function(x.off=0,y.off=0,a=1,b=NULL,th.off=0,th.max=2*pi,pts=36,...) {
  if (is.null(b)) b<-a
  th<-seq(0,th.max,length.out=pts)
  data.frame(x=a*cos(th.off)*cos(th)+b*sin(th.off)*sin(th)+x.off,
             y=-1*a*sin(th.off)*cos(th)+b*cos(th.off)*sin(th)+y.off,
             id=as.factor(paste(x.off,y.off,a,b,th.off,pts,sep=":")),...)
}
deform.ellipse.draw<-function(c.box) {
  create.ellipse.points(x.off=c.box$x[1],
                        y.off=c.box$y[1],
                        a=c.box$a[1],
                        b=c.box$b[1],
                        th.off=c.box$th[1],
                        col=c.box$col[1])                    
}
bbox.fun<-function(in.df) {
  ddply(in.df,.(val), function(c.cell) {
    c.cell.mean<-colMeans.df(c.cell[,c("x","y")])
    xmn<-emin(c.cell$x)
    xmx<-emax(c.cell$x)
    ymn<-emin(c.cell$y)
    ymx<-emax(c.cell$y)
    out.df<-cbind(c.cell.mean,
                  data.frame(xi=c(xmn,xmn,xmx,xmx,xmn),
                             yi=c(ymn,ymx,ymx,ymn,ymn),
                             xw=xmx-xmn,
                             yw=ymx-ymn
                  ))
  })
}

# since the edge of the pixel is 0.5 away from the middle of the pixel
emin<-function(...) min(...)-0.5
emax<-function(...) max(...)+0.5
extents.fun<-function(in.df) {
  ddply(in.df,.(val), function(c.cell) {
    c.cell.mean<-colMeans.df(c.cell[,c("x","y")])
    out.df<-cbind(c.cell.mean,data.frame(xmin=c(c.cell.mean$x,emin(c.cell$x)),
                                         xmax=c(c.cell.mean$x,emax(c.cell$x)),
                                         ymin=c(emin(c.cell$y),c.cell.mean$y),
                                         ymax=c(emax(c.cell$y),c.cell.mean$y)))
  })
}

common.image.path<-"../common"
qbi.file<-function(file.name) file.path(common.image.path,"figures",file.name)
qbi.data<-function(file.name) file.path(common.image.path,"data",file.name)

th_fillmap.fn<-function(max.val) scale_fill_gradientn(colours=rainbow(10),limits=c(0,max.val))

Quantitative Big Imaging

author: Kevin Mader date: 14 April 2016 width: 1440 height: 900 css: ../common/template.css transition: rotate

ETHZ: 227-0966-00L

Groups of Objects and Distributions

Course Outline

source('../common/schedule.R')

25th February - Introduction and Workflows
3rd March - Image Enhancement (A. Kaestner)
10th March - Basic Segmentation, Discrete Binary Structures
17th March - Advanced Segmentation
24th March - Analyzing Single Objects
7th April - Analyzing Complex Objects
14th April - Spatial Distribution
21st April - Statistics and Reproducibility
28th April - Dynamic Experiments
12th May - Scaling Up / Big Data
19th May - Guest Lecture - High Content Screening
26th May - Guest Lecture - Machine Learning / Deep Learning and More Advanced Approaches
2nd June - Project Presentations

Literature / Useful References

Books

Jean Claude, Morphometry with R
Online through ETHZ
Buy it
John C. Russ, “The Image Processing Handbook”,(Boca Raton, CRC Press)
Available online within domain ethz.ch (or proxy.ethz.ch / public VPN)
J. Weickert, Visualization and Processing of Tensor Fields
Online

Papers / Sites

Voronoi Tesselations
Ghosh, S. (1997). Tessellation-based computational methods for the characterization and analysis of heterogeneous microstructures. Composites Science and Technology, 57(9-10), 1187–1210
Wolfram Explanation
Self-Avoiding / Nearest Neighbor
Schwarz, H., & Exner, H. E. (1983). The characterization of the arrangement of feature centroids in planes and volumes. Journal of Microscopy, 129(2), 155–169.
Kubitscheck, U. et al. (1996). Single nuclear pores visualized by confocal microscopy and image processing. Biophysical Journal, 70(5), 2067–77.
Alignment / Distribution Tensor
Mader, K. et al (2013). A quantitative framework for the 3D characterization of the osteocyte lacunar system. Bone, 57(1), 142–154
Aubouy, M., et al. (2003). A texture tensor to quantify deformations. Granular Matter, 5, 67–70. Retrieved from http://arxiv.org/abs/cond-mat/0301018
Two point correlation
Dinis, L., et. al. (2007). Analysis of 3D solids using the natural neighbour radial point interpolation method. Computer Methods in Applied Mechanics and Engineering, 196(13-16)

Previously on QBI …

Image Enhancment
Highlighting the contrast of interest in images
Minimizing Noise
Understanding image histograms
Automatic Methods
Component Labeling
Single Shape Analysis
Complicated Shapes

Outline

Motivation (Why and How?)
Local Environment
Neighbors
Voronoi Tesselation
Distribution Tensor

Global Enviroment
Alignment
Self-Avoidance
Two Point Correlation Function

Metrics

We examine a number of different metrics in this lecture and additionally to classifying them as Local and Global we can define them as point and voxel-based operations.

Point Operations

Nearest Neighbor
Delaunay Triangulation
Distribution Tensor
Point (Center of Volume)-based Voronoi Tesselation
Alignment

kable(data.frame(x=round(4*runif(4)),y=round(4*runif(4)), z=round(4*runif(4))))

x	y	z
0	2	1
2	3	4
3	1	2
2	2	2

Voxel Operation

Voronoi Tesselation
Neighbor Counting
2-point (N-point) correlation functions

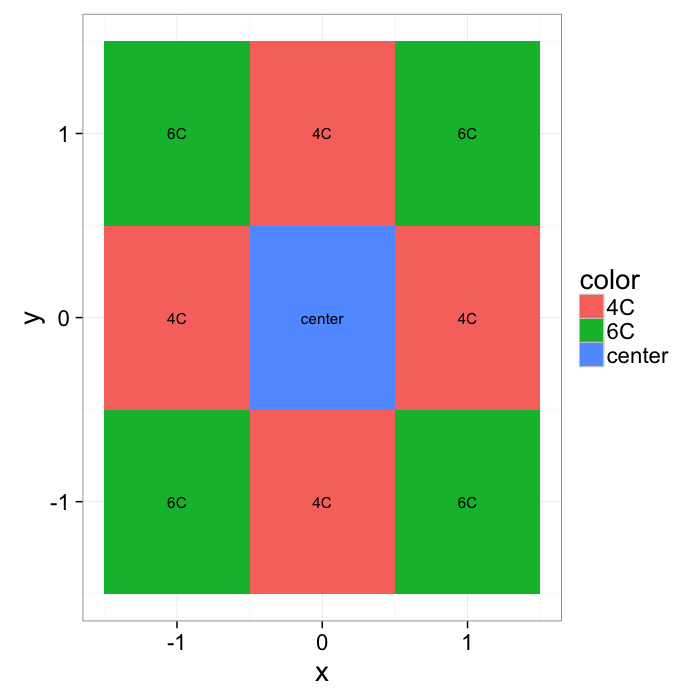
xymesh<-mutate(
  expand.grid(x=c(-1:1),y=c(-1:1)),
  color=ifelse((x==0) & (y==0),"center",ifelse(sqrt(x^2+y^2)==1,"4C","6C"))
  )
ggplot(xymesh,aes(x,y,fill=color))+
  geom_tile()+
  geom_text(aes(label=color))+
  labs(color="")+
  theme_bw(20)

What do we start with?

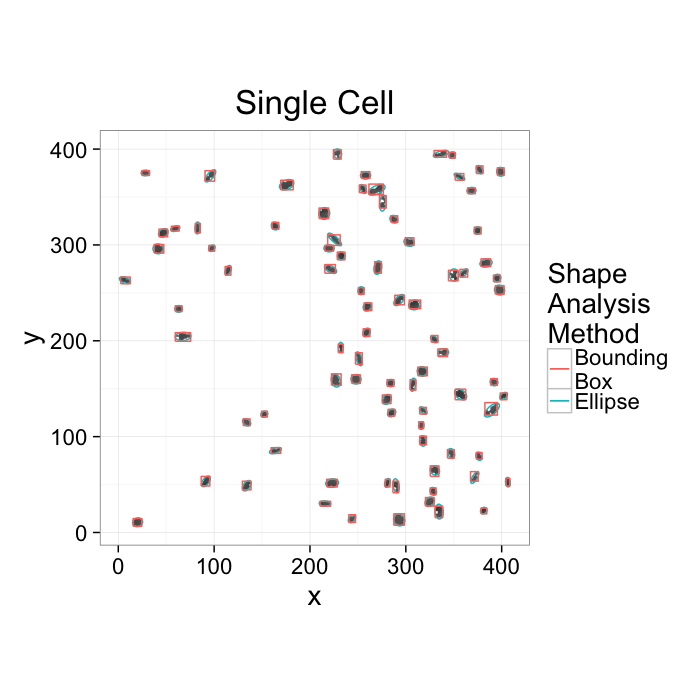
Going back to our original cell image

We have been able to get rid of the noise in the image and find all the cells (lecture 2-4)
We have analyzed the shape of the cells using the shape tensor (lecture 5)
We even separated cells joined together using Watershed (lecture 6)

We can characterize the sample and the average and standard deviations of volume, orientation, surface area, and other metrics

Motivation (Why and How?)

With all of these images, the first step is always to understand exactly what we are trying to learn from our images.

cell.im<-jpeg::readJPEG("ext-figures/Cell_Colony.jpg")
cell.lab.df<-im.to.df(bwlabel(cell.im<.6))
size.histogram<-ddply(subset(cell.lab.df,val>0),.(val),function(c.label) data.frame(count=nrow(c.label)))
keep.vals<-subset(size.histogram,count>25)


cur.cell.df<-subset(cell.lab.df,val %in% keep.vals$val)
cell.pca<-pca.fun(cur.cell.df)
cell.ellipse<-vec.to.ellipse(cell.pca)
ggplot(cur.cell.df,aes(x=x,y=y))+
  geom_tile(color="black",fill="grey")+
  geom_path(data=cell.ellipse,aes(color="Ellipse",group=val))+
  geom_path(data=bbox.fun(cur.cell.df),aes(x=xi,y=yi,color="Bounding\nBox",group=val))+
  labs(title="Single Cell",color="Shape\nAnalysis\nMethod")+
  theme_bw(20)+coord_equal()+guides(fill=F)

We want to know how many cells are alive

Maybe small cells are dead and larger cells are alive → examine the volume distribution
Maybe living cells are round and dead cells are really spiky and pointy → examine anisotropy

We want to know where the cells are alive or most densely packed

We can visually inspect the sample (maybe even color by volume)
We can examine the raw positions (x,y,z) but what does that really tell us?
We can make boxes and count the cells inside each one
How do we compare two regions in the same sample or even two samples?

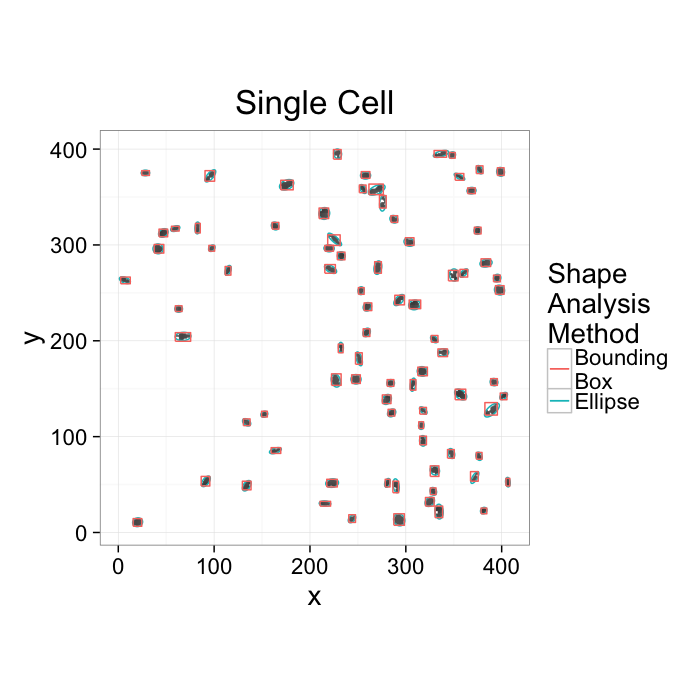
Motivation (continued)

ggplot(cur.cell.df,aes(x=x,y=y))+
  geom_tile(color="black",fill="grey")+
  geom_path(data=cell.ellipse,aes(color="Ellipse",group=val))+
  geom_path(data=bbox.fun(cur.cell.df),aes(x=xi,y=yi,color="Bounding\nBox",group=val))+
  labs(title="Single Cell",color="Shape\nAnalysis\nMethod")+
  theme_bw(20)+coord_equal()+guides(fill=F)

We want to know how the cells are communicating

Maybe physically connected cells (touching) are communicating → watershed
Maybe cells oriented the same direction are communicating → average? orientation
Maybe cells which are close enough are communicating → ?
Maybe cells form hub and spoke networks → ?

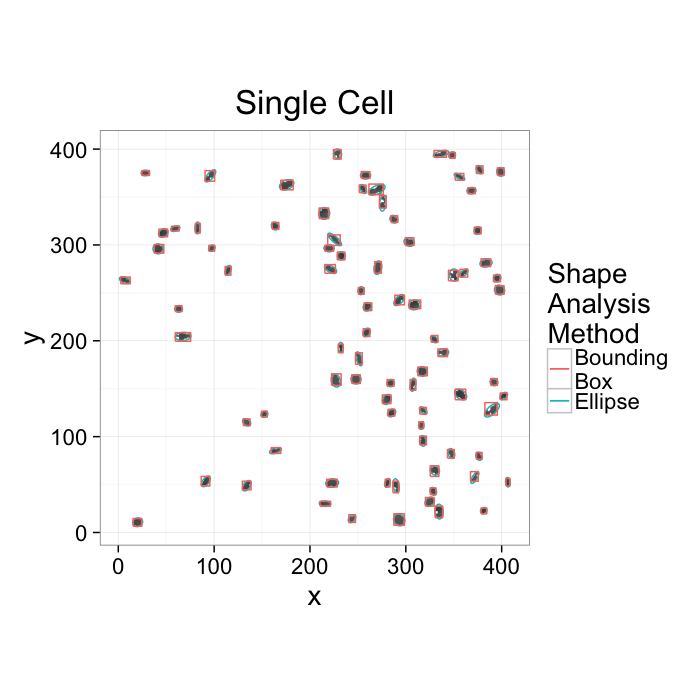
Motivation (continued)

ggplot(cur.cell.df,aes(x=x,y=y))+
  geom_tile(color="black",fill="grey")+
  geom_path(data=cell.ellipse,aes(color="Ellipse",group=val))+
  geom_path(data=bbox.fun(cur.cell.df),aes(x=xi,y=yi,color="Bounding\nBox",group=val))+
  labs(title="Single Cell",color="Shape\nAnalysis\nMethod")+
  theme_bw(20)+coord_equal()+guides(fill=F)

We want to know how the cells are nourished

Maybe closely packed cells are better nourished → count cells in a box__?__
Maybe cells are oriented around canals which supply them → ?

So what do we still need

A way for counting cells in a region and estimating density without creating arbitrary boxes
A way for finding out how many cells are near a given cell, it’s nearest neighbors
A way for quantifying how far apart cells are and then comparing different regions within a sample
A way for quantifying and comparing orientations

What would be really great?

A tool which could be adapted to answering a large variety of problems

multiple types of structures
multiple phases

Destructive Measurements

With most imaging techniques and sample types, the task of measurement itself impacts the sample.

Even techniques like X-ray tomography which claim to be non-destructive still impart significant to lethal doses of X-ray radition for high resolution imaging
Electron microscopy, auto-tome-based methods, histology are all markedly more destructive and make longitudinal studies impossible
Even when such measurements are possible
Registration can be a difficult task and introduce artifacts

Why is this important?

techniques which allow us to compare different samples of the same type.
are sensitive to common transformations
Sample B after the treatment looks like Sample A stretched to be 2x larger
The volume fraction at the center is higher than the edges but organization remains the same

Ok, so now what?

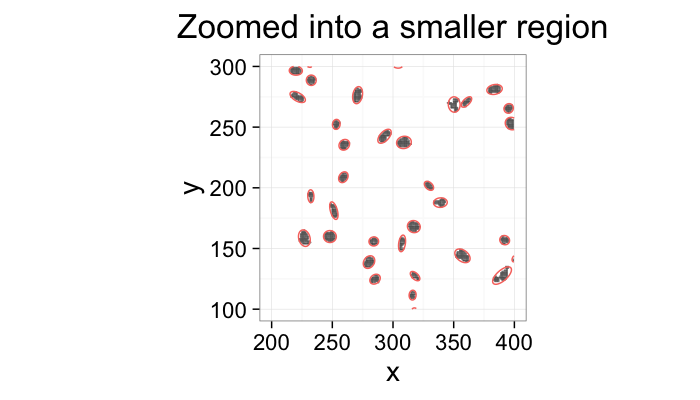
ggplot(cur.cell.df,aes(x=x,y=y))+
  geom_tile(color="black",fill="grey")+
  geom_path(data=cell.ellipse,aes(color="Ellipse",group=val))+
  labs(title="Zoomed into a smaller region")+
  xlim(200,400)+ylim(100,300)+
  theme_bw(20)+coord_equal()+guides(fill=F,color=F)

↓

kable(head(cell.pca[,c("x","y","vx","vy")]),align='c',digits=2)

x	y	vx	vy
20.19	10.69	-0.95	-0.30
20.19	10.69	0.30	-0.95
293.08	13.18	-0.50	0.86
293.08	13.18	-0.86	-0.50
243.81	14.23	0.68	0.74
243.81	14.23	-0.74	0.68

⋯
***

So if we want to know the the mean or standard deviations of the position or orientations we can analyze them easily.

cell.pca$Theta<-cell.pca$th.off*180/pi
cell.pca$Length<-cell.pca$vw
s.table<-apply(cell.pca[,c("x","y","Length","vx","vy","Theta")],2,summary)

kable(t(s.table),align='c',digits=2)

	Min.	1st Qu.	Median	Mean	3rd Qu.	Max.
x	6.90	215.70	280.50	258.20	339.00	406.50
y	10.69	111.60	221.00	208.60	312.50	395.20
Length	1.06	1.57	1.95	2.08	2.41	4.33
vx	-1.00	-0.94	-0.70	-0.42	0.07	0.71
vy	-1.00	-0.70	0.02	0.04	0.71	1.00
Theta	-180.00	-134.10	-0.50	-4.67	130.60	177.70

But what if we want more or other information?

Simple Statistics

When given a group of data, it is common to take a mean value since this is easy. The mean bone thickness is 0.3mm. This is particularly relevant for groups with many samples because the mean is much smaller than all of the individual points.

but means can lie

the mean of 0^∘ and 180^∘ = 90^∘
the distance between -180^∘ and 179^∘ is 359^∘
since we have not defined a tip or head, 0^∘ and 180^∘ are actually the same

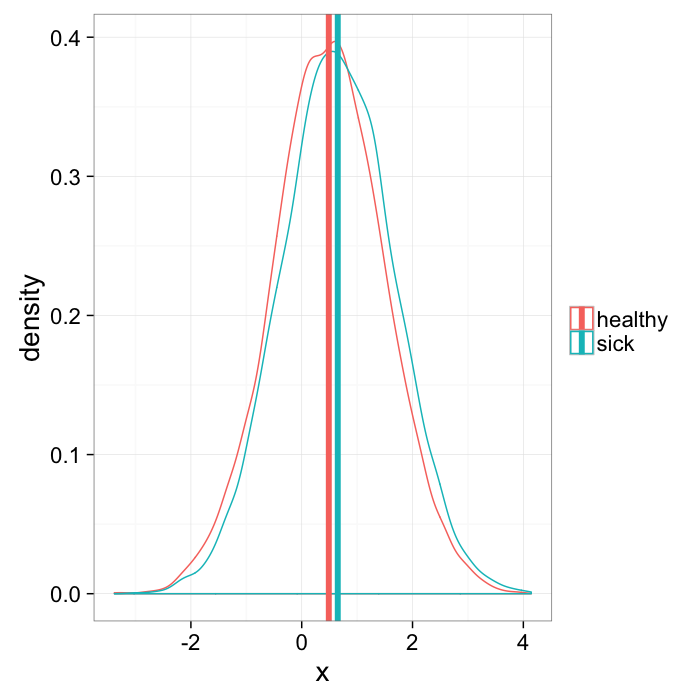
some means are not very useful

mean.example<-rbind(
    data.frame(x=rnorm(10000,mean=0.5),group="healthy"),
    data.frame(x=rnorm(10000,mean=0.65),group="sick")
  )
mean.means<-ddply(mean.example,.(group),function(x) data.frame(mean.x=mean(x$x)))
ggplot(mean.example,aes(x=x,colour=group))+
  geom_density()+
  geom_vline(data=mean.means,aes(xintercept=mean.x,colour=group),size=2)+
  labs(color="")+
  theme_bw(20)

Calculating Density

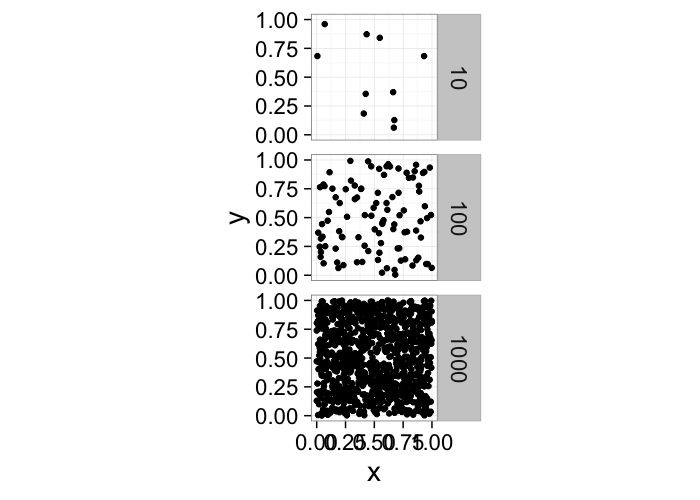
One of the first metrics to examine with distribution is density → how many objects in a given region or volume.

It is deceptively easy to calculate involving the ratio of the number of objects divided by the volume.

pt.maker<-function(n.pts,rn.fun=function(pts) runif(pts,min=0,max=1),...) data.frame(x=rn.fun(n.pts),y=rn.fun(n.pts),n.pts=n.pts,...)

ggplot(ldply(c(10,100,1000),pt.maker),aes(x,y))+
  geom_point()+facet_grid(n.pts~.)+
  coord_equal()+
  theme_bw(20)

It doesn’t tell us much, many very different systems with the same density and what if we want the density of a single point? Does that even make sense?

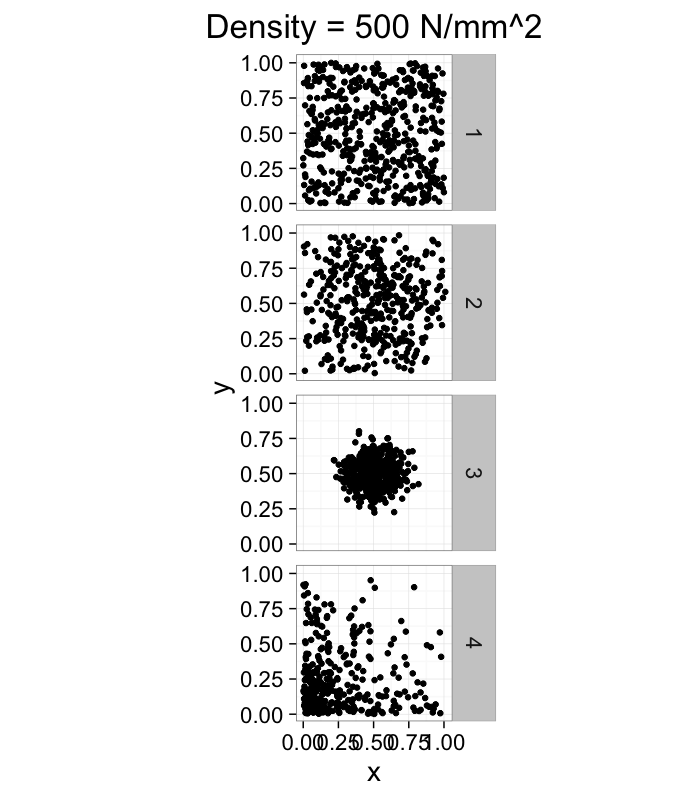
dist.funs<-c(function(pts) runif(pts,min=0,max=1),
             function(pts) rnorm(pts,mean=0.5,sd=0.3),
             function(pts) rnorm(pts,mean=0.5,sd=0.1),
             function(pts) rlnorm(pts,meanlog=1.5,sdlog=1.5)/exp(3))

ggplot(ldply(1:length(dist.funs),function(fun.ind) pt.maker(500,rn.fun=dist.funs[[fun.ind]],fun.ind=fun.ind)),
       aes(x,y))+
  geom_point()+facet_grid(fun.ind~.)+
  coord_equal()+
  xlim(0,1.01)+ylim(0,1.01)+
  labs(title="Density = 500 N/mm^2")+
  theme_bw(20)

Neighbors

Definition

Oxford American → be situated next to or very near to (another)

Does not sound very scientific
How close?
Touching, closer than anything else?

Nearest Neighbor (distance)

find.nn<-function(in.df) {
  ddply(in.df,.(val),function(c.group) {
    cur.val<-c.group$val[1]
    cur.x<-c.group$x[1]
    cur.y<-c.group$y[1]
    all.butme<-subset(in.df,val!=cur.val)
    all.butme$dist<-with(all.butme,sqrt((x-cur.x)^2+(y-cur.y)^2))
    min.ele<-subset(all.butme,dist<=min(all.butme$dist))
    min.ele.order<-order(runif(nrow(min.ele)))
    min.ele<-min.ele[min.ele.order,]
    out.df<-data.frame(x=cur.x,y=cur.y,
               xe=min.ele$x[1],ye=min.ele$y[1],vale=min.ele$val[1],dist=min.ele$dist[1])
    out.df
    })
}

Given a set of objects with centroids at
$\textbf{P}=\begin{bmatrix} \vec{x}_0,\vec{x}_1,\cdots,\vec{x}_i \end{bmatrix}$

We can define the nearest neighbor as the position of the object in our set which is closest

$\vec{\textrm{NN}}(\vec{y}) = \textrm{argmin}(||\vec{y}-\vec{x}|| \forall \vec{x} \in \textbf{P}-\vec{y})$

We define the distance as the Euclidean distance from the current point to that point, and the angle as the

$\textrm{NND}(\vec{y}) = \textrm{min}(||\vec{y}-\vec{x}|| \forall \vec{x} \in \textbf{P}-\vec{y})$

$\textrm{NN}\theta(\vec{y}) = \tan^{-1}\frac{(\vec{\textrm{NN}}-\vec{y})\cdot \vec{j}}{(\vec{\textrm{NN}}-\vec{y})\cdot \vec{i}}$

Nearest Neighbor Definition

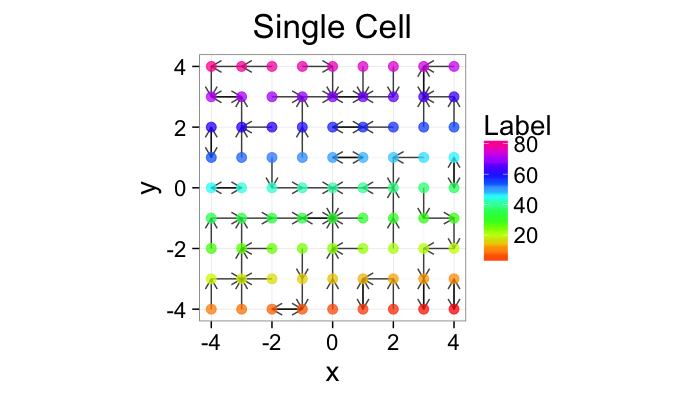
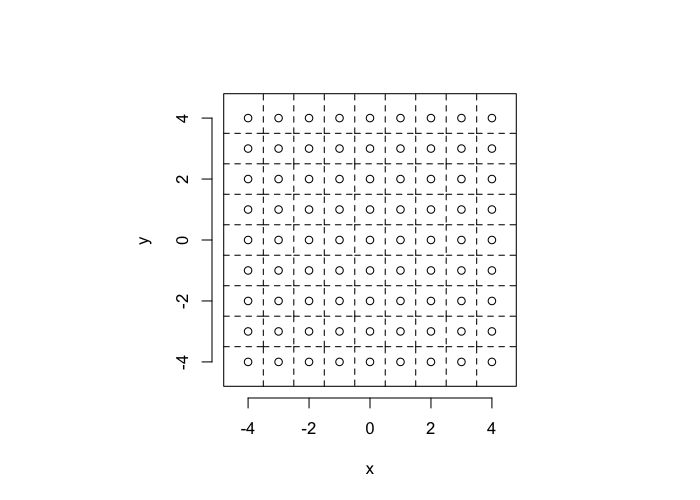
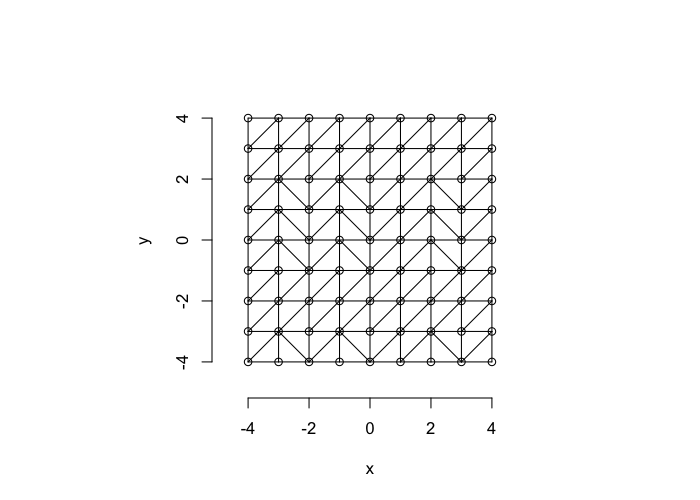
So examining a simple starting system like a grid, we already start running into issues.

In a perfect grid like structure each object has 4 equidistant neighbors (6 in 3D)
Which one is closest?

We thus add an additional clause (only relevant for simulated data) where if there are multiple equidistant neighbors, a nearest is chosen randomly

This ensures when we examine the orientation distribution (NNθ) of the neighbors it is evenly distributed

cur.grid<-expand.grid(x=-c(-4:4),y=c(-4:4))
cur.grid$val<-1:nrow(cur.grid)
std.grid<-cur.grid
ggplot(cur.grid,aes(x=x,y=y))+
  geom_segment(data=find.nn(cur.grid),aes(xend=xe,yend=ye),
               arrow=arrow(length = unit(0.3,"cm")),alpha=0.75)+
  geom_point(aes(color=val),size=3,alpha=0.75)+
  labs(title="Single Cell",color="Label")+
  scale_color_gradientn(colours=rainbow(10))+
  coord_equal()+
  theme_bw(20)+guides(fill=F)

In-Silico Systems

For the rest of these sections we will repeatedly use several simple in-silico systems to test our methods and try to better understand the kind of results we obtain from them.

Compression
The most simple system simply involves a scaling in every direction by α
α < 1 the system is compressed
α > 1 the system is expanded

$\begin{bmatrix} x^\prime \\ y^\prime \end{bmatrix} = \alpha \begin{bmatrix} x \\ y \end{bmatrix}$

Shearing
Slightly more complicated system where objects are shifted based on their location using a slope of α

$\begin{bmatrix} x^\prime \\ y^\prime \end{bmatrix} = \begin{bmatrix} 1 & \alpha \\ 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}$

In-Silico Systems (Continued)

Stretch
A non-evenly distributed system with a parameter α controlling if objects bunch near the edges or the center. A maximum distance m is defined as the magnitude of the largest offset in x or y
+ Same total volume just arranged differently

$\begin{bmatrix} x^\prime \\ y^\prime \end{bmatrix} = \begin{bmatrix} \textrm{sign}(x) \left(\frac{|x|}{m}\right)^\alpha m \\ \textrm{sign}(y) \left(\frac{|y|}{m}\right)^\alpha m \end{bmatrix}$

Swirl
A transformation where the points are rotated more based on how far away they are from the center and the slope of the swirl (α),

$\theta (x,y) = \alpha \sqrt{x^2+y^2}$

$\begin{bmatrix} x^\prime \\ y^\prime \end{bmatrix} = \begin{bmatrix} \cos\theta(x,y) & -\sin\theta(x,y) \\ \sin\theta(x,y) & \cos\theta(x,y) \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}$

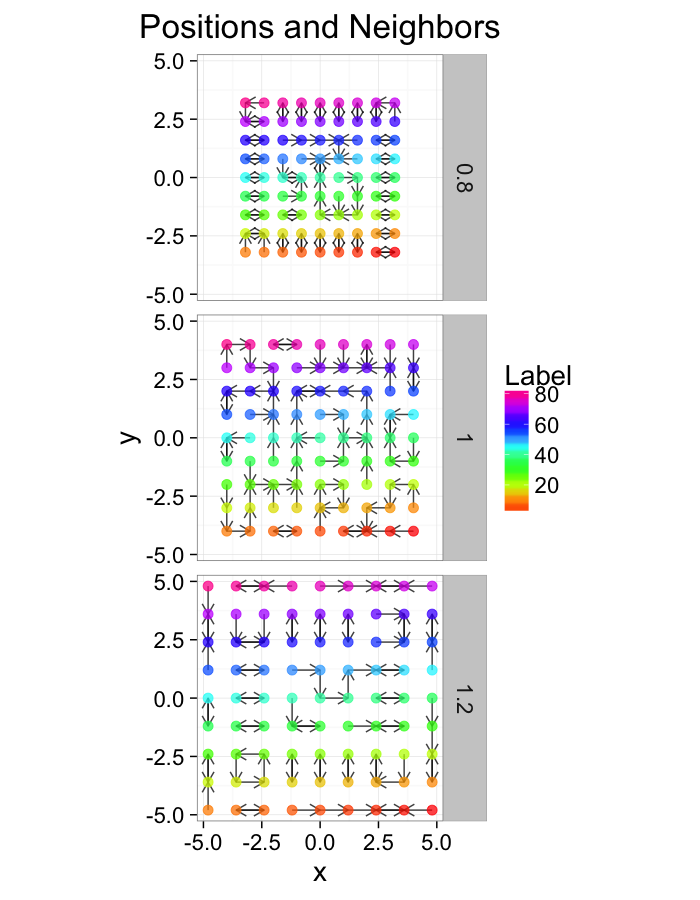
Examining Compression

comp.fun<-function(c.stretch,in.grid=cur.grid) {
  str.grid<-in.grid
  str.grid$x<-with(in.grid,c.stretch*x)
  str.grid$y<-with(in.grid,c.stretch*y)
  cbind(str.grid,glab=c.stretch)
}
test.systems.comp<-ldply(c(0.8,1,1.2),comp.fun)

dist.plots.comp<-ddply(test.systems.comp,.(glab),find.nn)
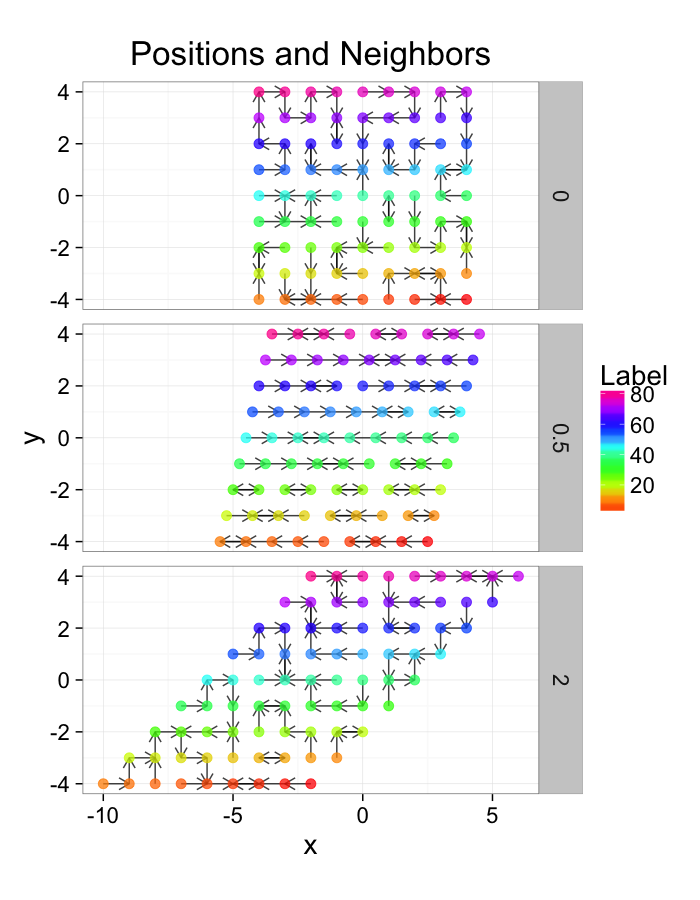
ggplot(test.systems.comp,aes(x=x,y=y))+
  geom_segment(data=dist.plots.comp,aes(xend=xe,yend=ye),
               arrow=arrow(length = unit(0.3,"cm")),alpha=0.75)+
  geom_point(aes(color=val),size=3,alpha=0.75)+
  labs(title="Positions and Neighbors",color="Label")+
  scale_color_gradientn(colours=rainbow(10))+
    coord_equal()+
  facet_grid(glab~.)+
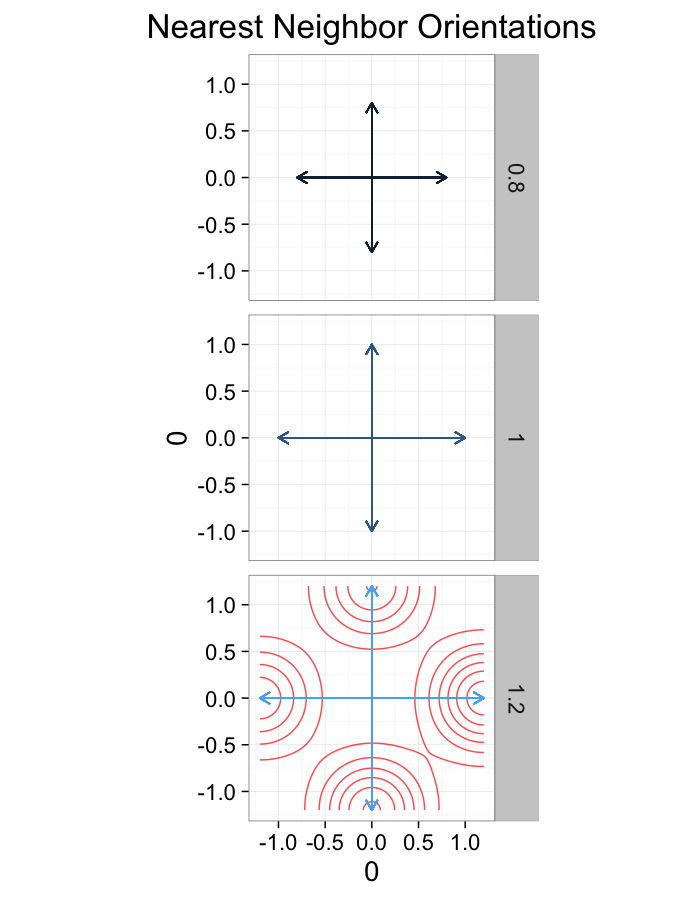
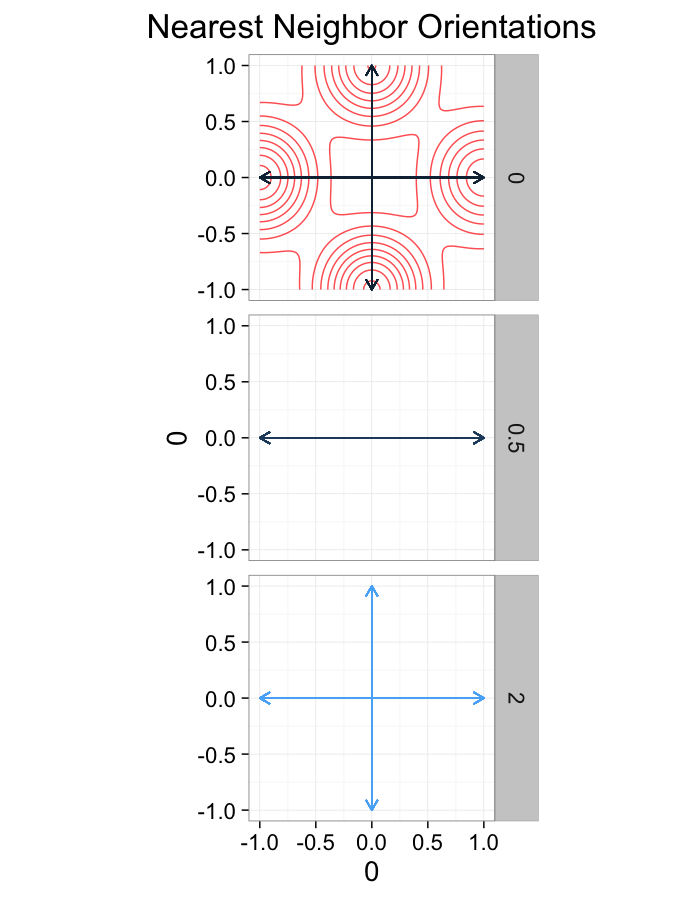
  theme_bw(20)

ggplot(dist.plots.comp,
       aes(x=0,y=0,xend=xe-x,yend=ye-y))+
    geom_density2d(aes(x=xe-x,y=ye-y),color="red",alpha=0.7)+
  geom_segment(aes(color=glab),
               arrow=arrow(length = unit(0.3,"cm")))+
  facet_grid(glab~.)+
    coord_equal()+
  labs(title="Nearest Neighbor Orientations")+guides(color=F)+
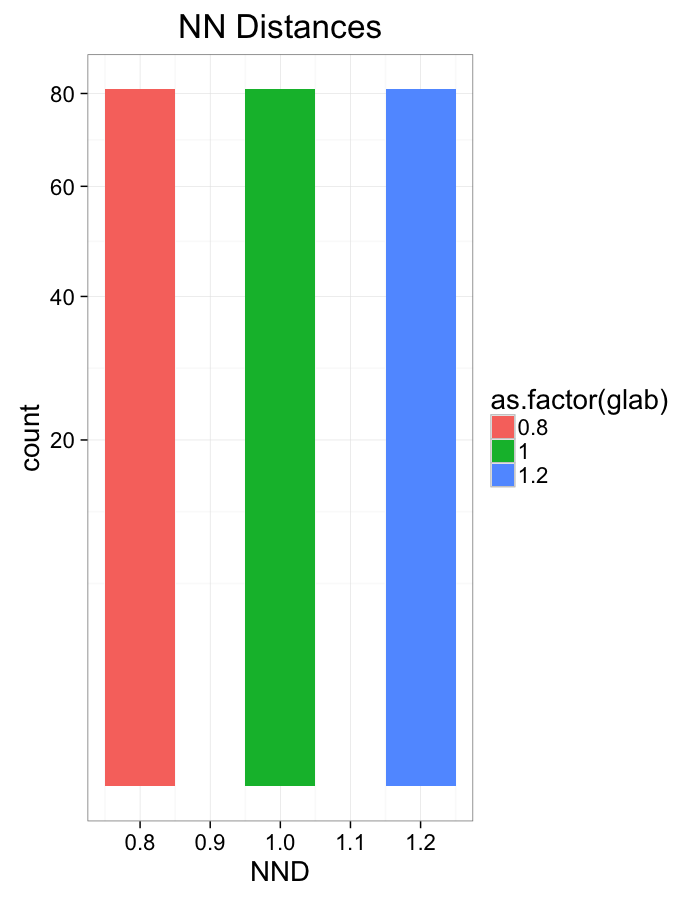
  theme_bw(20)

Compression Distributions

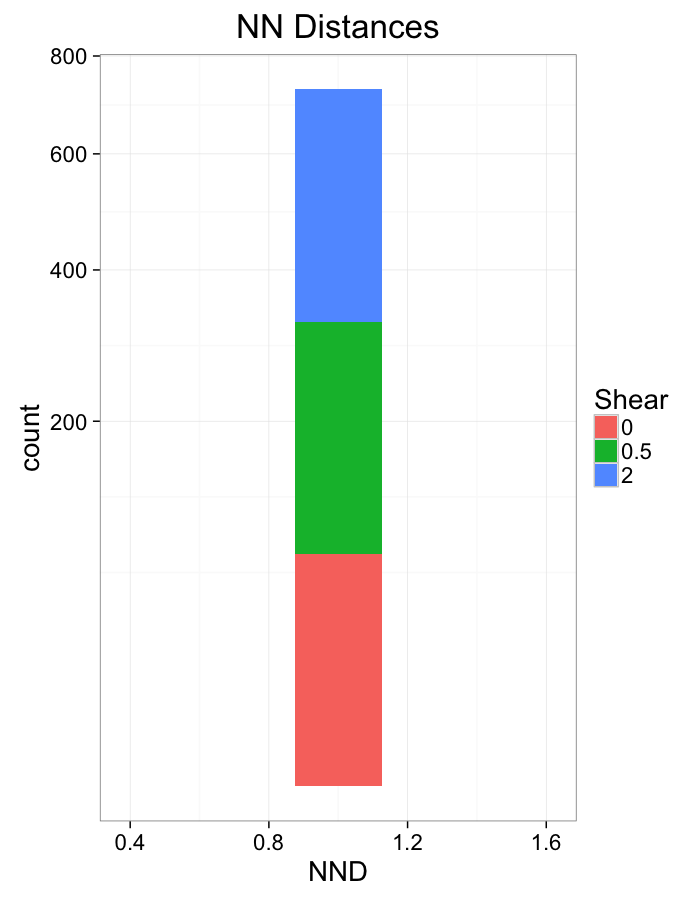
ggplot(dist.plots.comp,      
       aes(x=dist,fill=as.factor(glab)))+
  geom_histogram(binwidth=0.1)+
  labs(x="NND",title="NN Distances",color="Stretch")+
  scale_y_sqrt()+
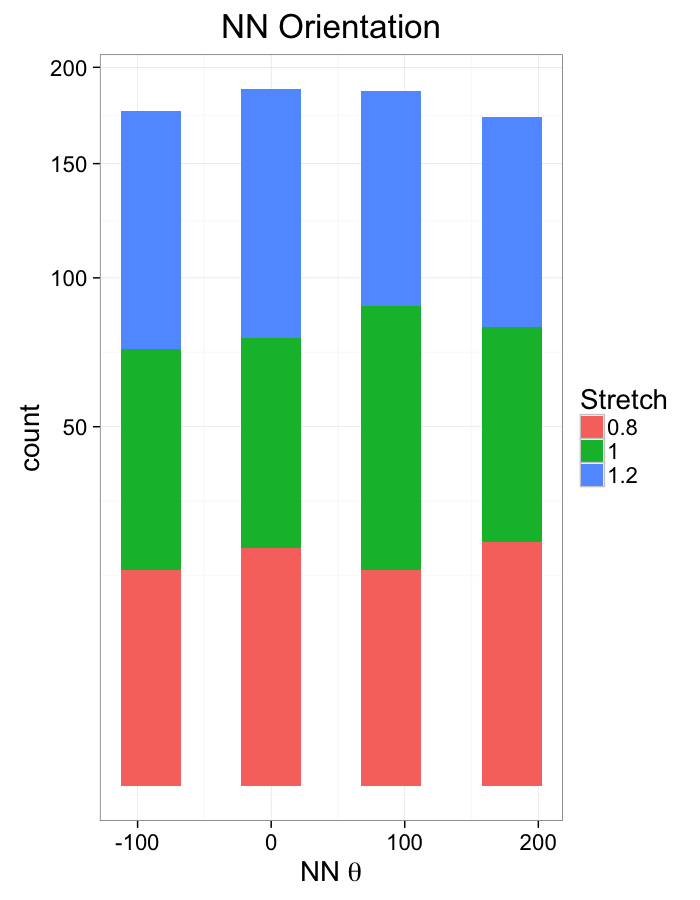
  theme_bw(20)

ggplot(dist.plots.comp,      
       aes(x=180/pi*atan2(ye-y,xe-x),fill=as.factor(glab)))+
  geom_histogram(binwidth=45)+
    labs(x=expression(paste("NN ",theta)),title="NN Orientation",fill="Stretch")+
  scale_y_sqrt()+
  theme_bw(20)

Examining Different Shears

shear.fun<-function(c.shear,in.grid=cur.grid) {
  str.grid<-in.grid
  str.grid$x<-with(in.grid,x+c.shear*(y-2)/2)
  cbind(str.grid,glab=c.shear)
}
test.systems.shear<-ldply(c(0,0.5,2),shear.fun)

dist.plots.shear<-ddply(test.systems.shear,.(glab),find.nn)
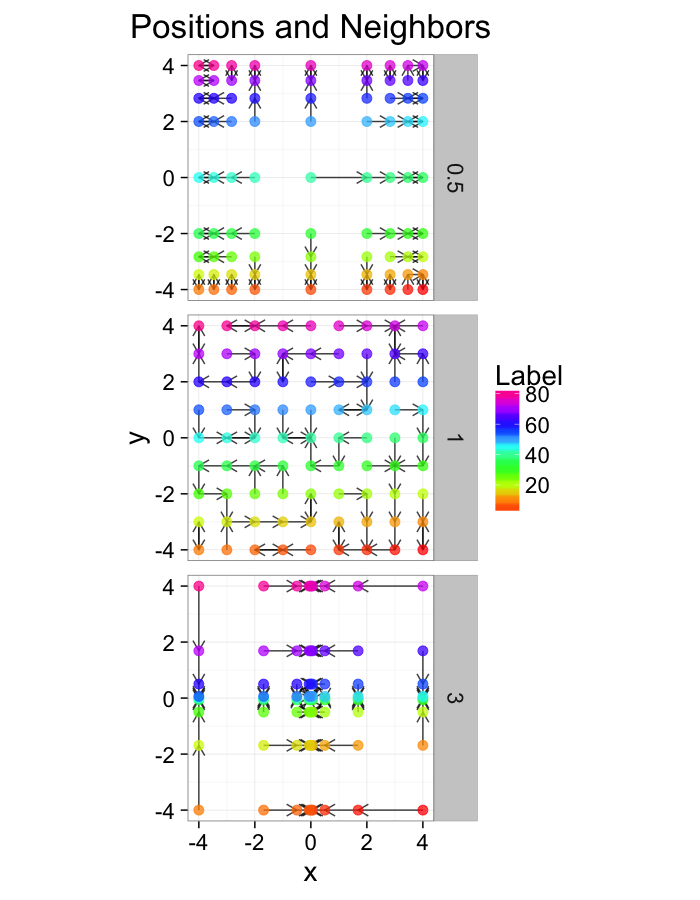
ggplot(test.systems.shear,aes(x=x,y=y))+
  geom_segment(data=dist.plots.shear,aes(xend=xe,yend=ye),
               arrow=arrow(length = unit(0.3,"cm")),alpha=0.75)+
  geom_point(aes(color=val),size=3,alpha=0.75)+
  labs(title="Positions and Neighbors",color="Label")+
  scale_color_gradientn(colours=rainbow(10))+
    coord_equal()+
  facet_grid(glab~.)+
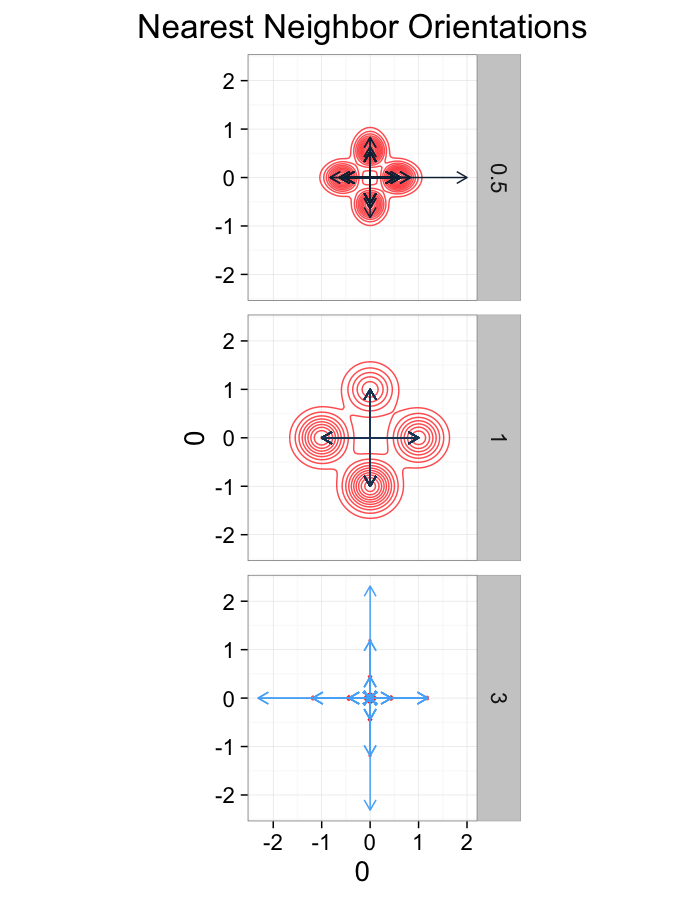
  theme_bw(20)

ggplot(dist.plots.shear,
       aes(x=0,y=0,xend=xe-x,yend=ye-y))+
    geom_density2d(aes(x=xe-x,y=ye-y),color="red",alpha=0.7)+
  geom_segment(aes(color=glab),
               arrow=arrow(length = unit(0.3,"cm")))+
  facet_grid(glab~.)+
    coord_equal()+
  labs(title="Nearest Neighbor Orientations")+guides(color=F)+
  theme_bw(20)

Shear Distributions

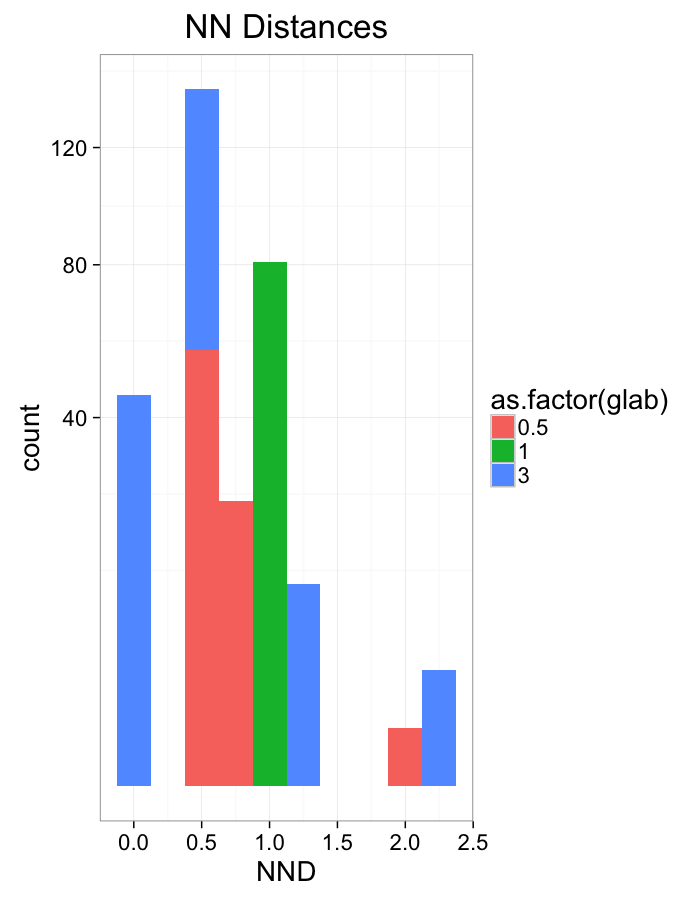
ggplot(dist.plots.shear,      
       aes(x=dist,fill=as.factor(glab)))+
  geom_histogram(binwidth=0.25)+
  labs(x="NND",title="NN Distances",fill="Shear")+
  scale_y_sqrt()+
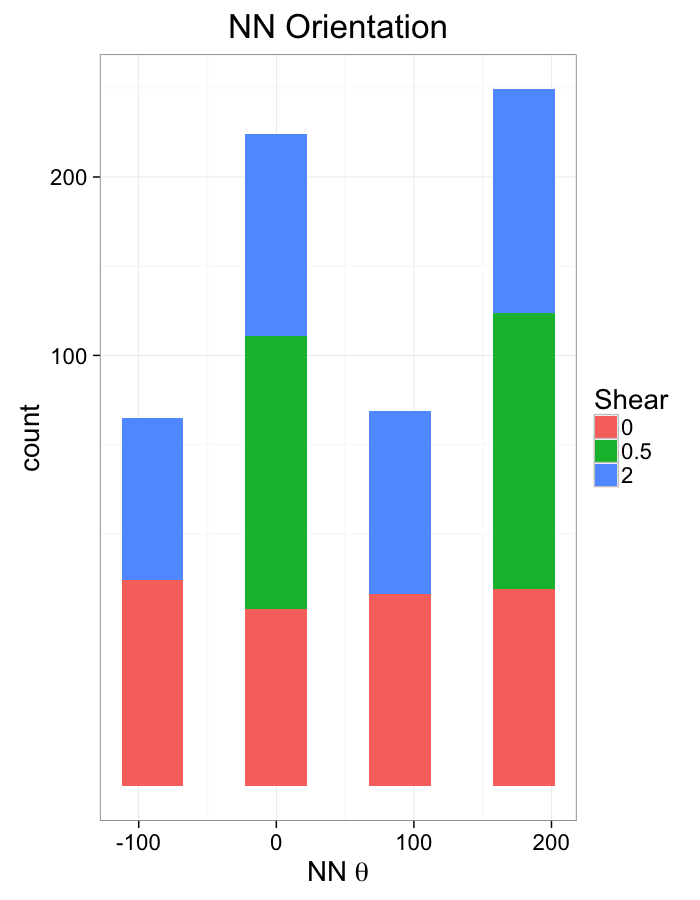
  theme_bw(20)

ggplot(dist.plots.shear,      
       aes(x=180/pi*atan2(ye-y,xe-x),fill=as.factor(glab)))+
  geom_histogram(binwidth=45)+
    labs(x=expression(paste("NN ",theta)),title="NN Orientation",fill="Shear")+
  scale_y_sqrt()+
  theme_bw(20)

Examining Different Stretches

str.fun<-function(x,a=1,r=4) sign(x)*r*(abs(x)/r)^a
stretch.fun<-function(c.stretch,in.grid=cur.grid) {
  str.grid<-in.grid
  str.grid$x<-with(in.grid,str.fun(x,a=c.stretch))
  str.grid$y<-with(in.grid,str.fun(y,a=c.stretch))
  cbind(str.grid,glab=c.stretch)
}
test.systems<-ldply(c(0.5,1,3),stretch.fun)

dist.plots<-ddply(test.systems,.(glab),find.nn)
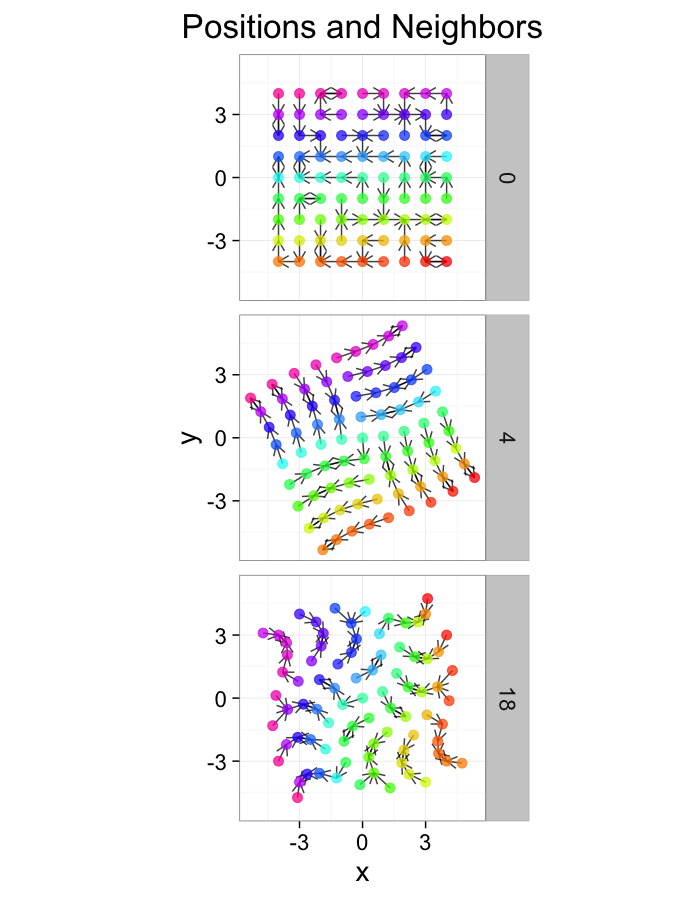
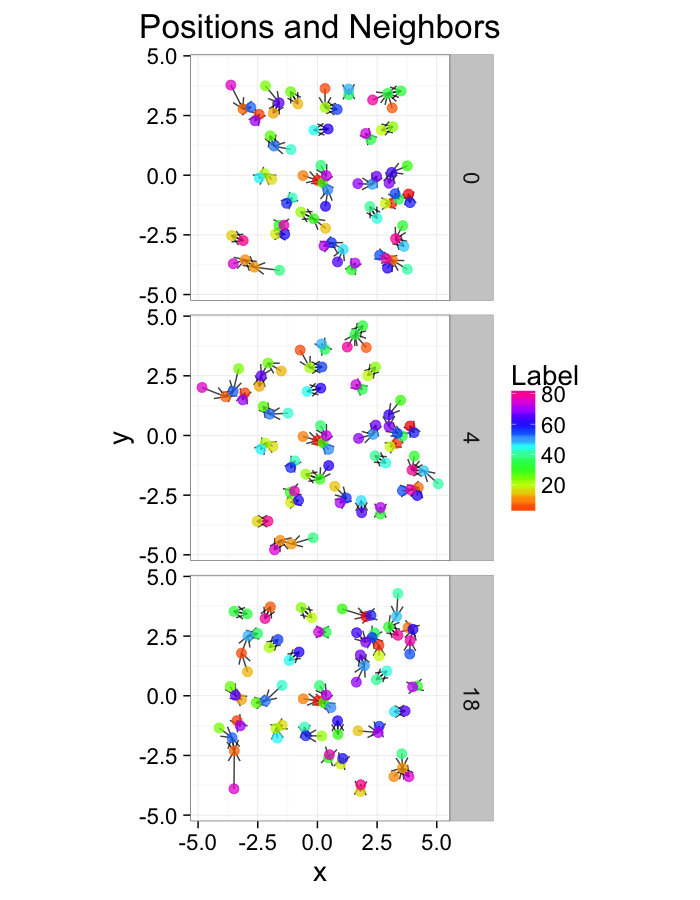
ggplot(test.systems,aes(x=x,y=y))+
  geom_segment(data=dist.plots,aes(xend=xe,yend=ye),
               arrow=arrow(length = unit(0.3,"cm")),alpha=0.75)+
  geom_point(aes(color=val),size=3,alpha=0.75)+
  labs(title="Positions and Neighbors",color="Label")+
  scale_color_gradientn(colours=rainbow(10))+
    coord_equal()+
  facet_grid(glab~.)+
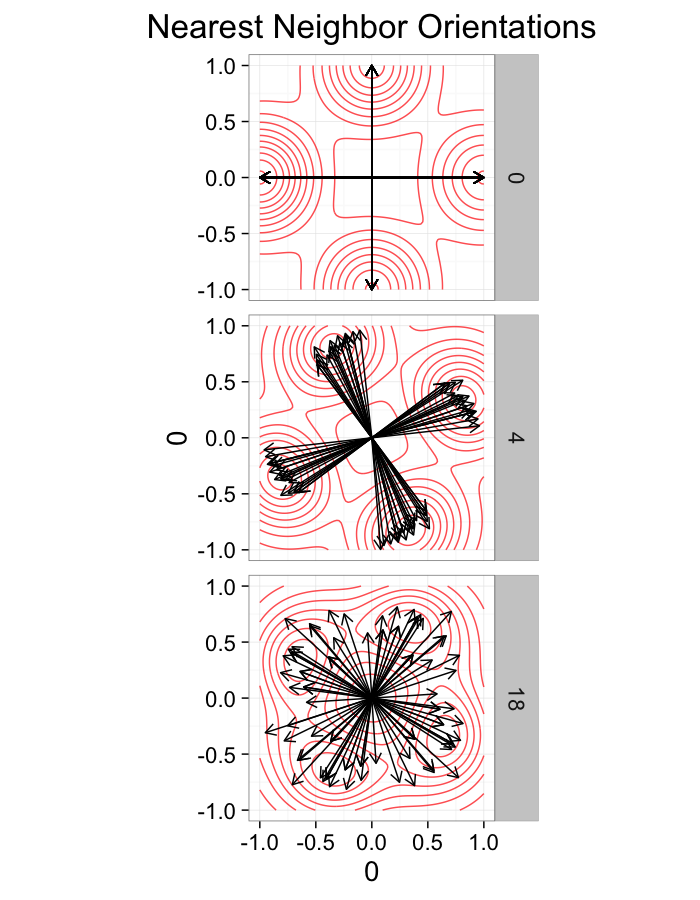
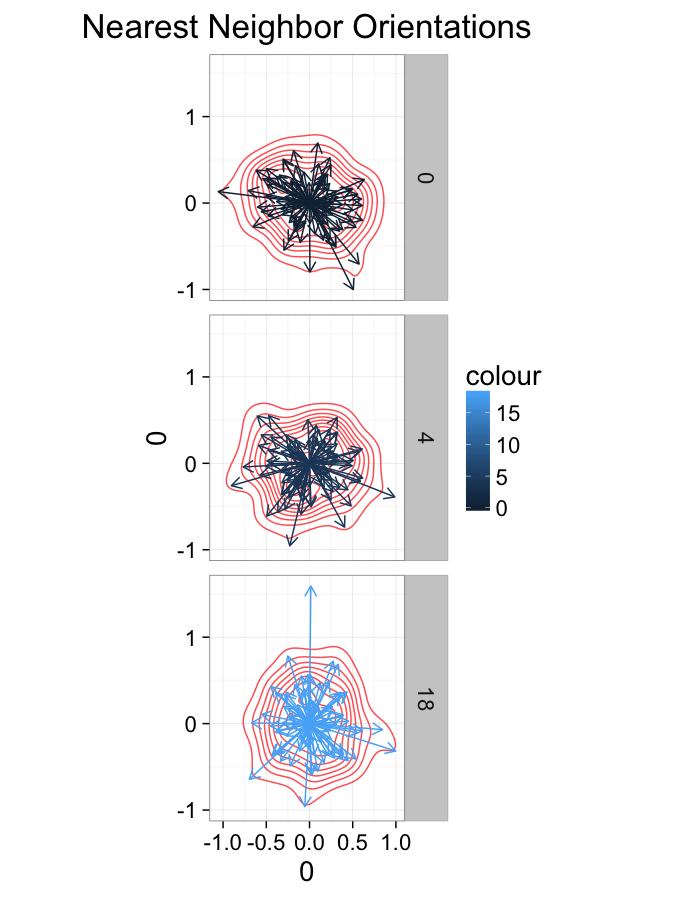
  theme_bw(20)

ggplot(dist.plots,
       aes(x=0,y=0,xend=xe-x,yend=ye-y))+
    geom_density2d(aes(x=xe-x,y=ye-y),color="red",alpha=0.7)+
  geom_segment(aes(color=glab),
               arrow=arrow(length = unit(0.3,"cm")))+
  facet_grid(glab~.)+
    coord_equal()+
  labs(title="Nearest Neighbor Orientations")+guides(color=F)+
  theme_bw(20)

Stretch Distributions

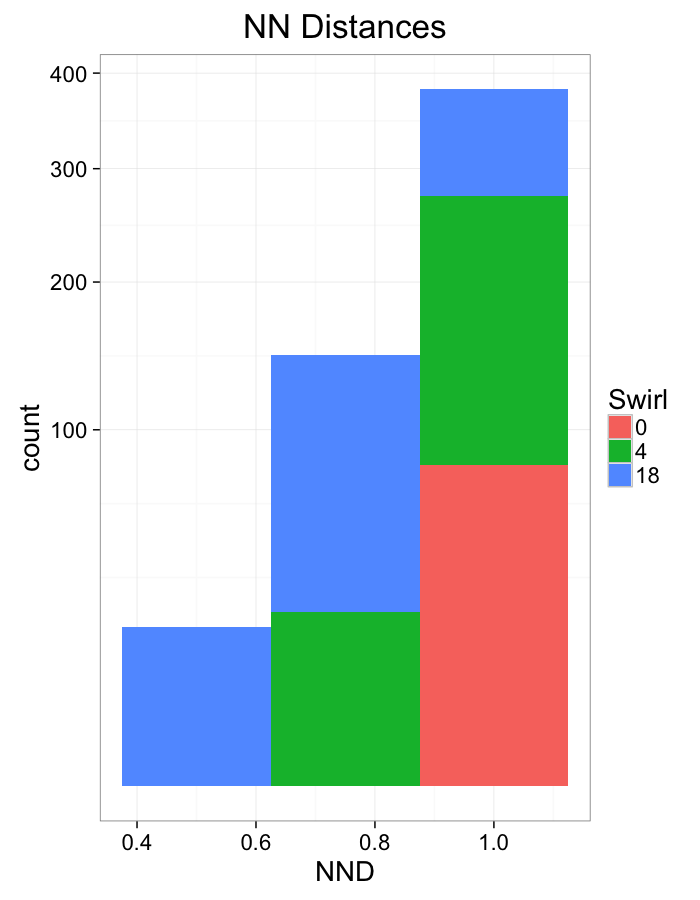
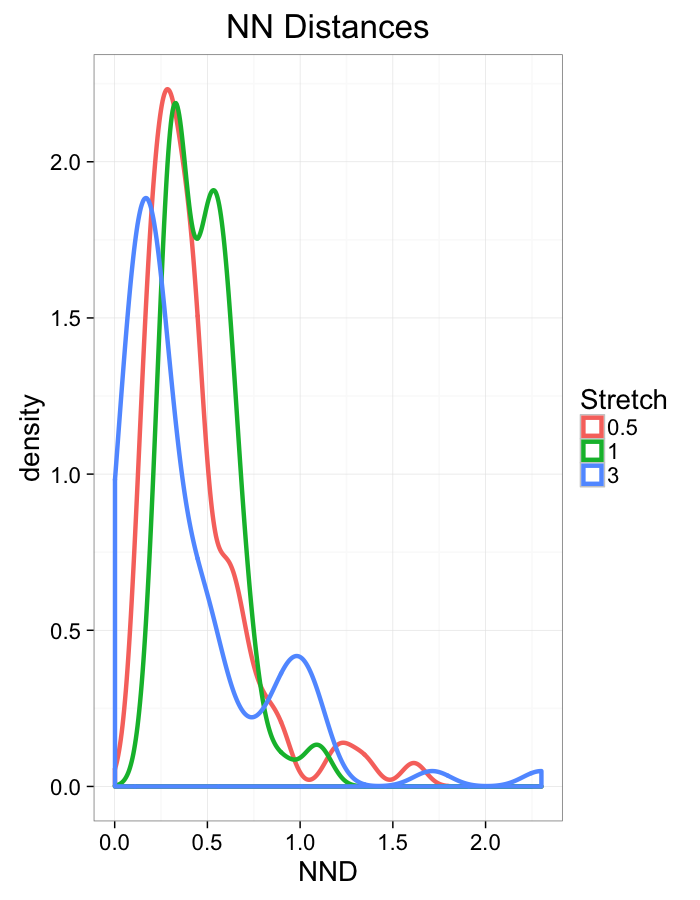
ggplot(dist.plots,      
       aes(x=dist,fill=as.factor(glab)))+
  #geom_density(size=1.5,adjust=1/5)+
  geom_histogram(binwidth=0.25)+
  labs(x="NND",title="NN Distances",color="Stretch")+
  scale_y_sqrt()+
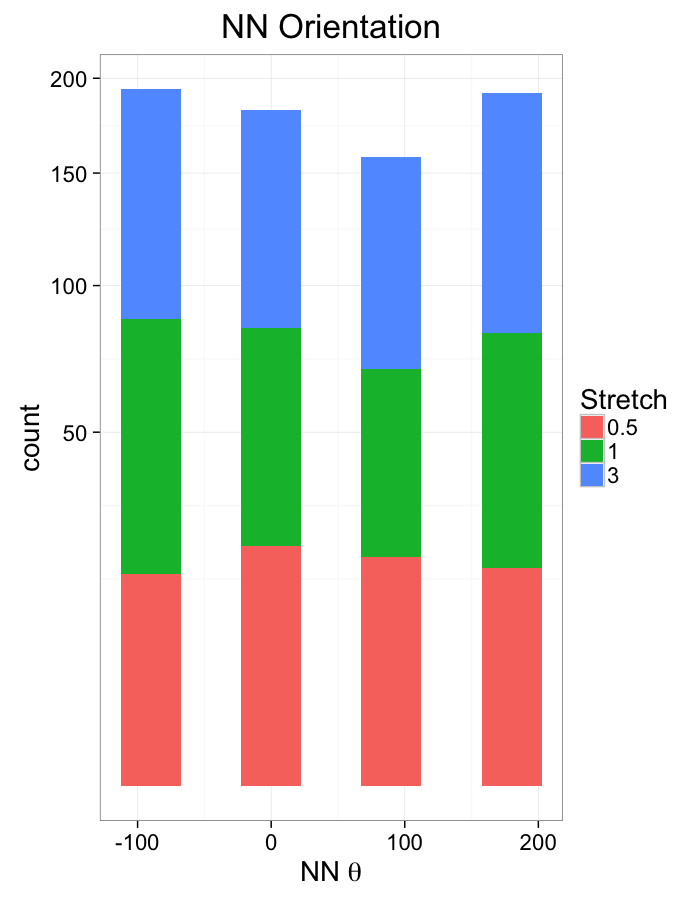
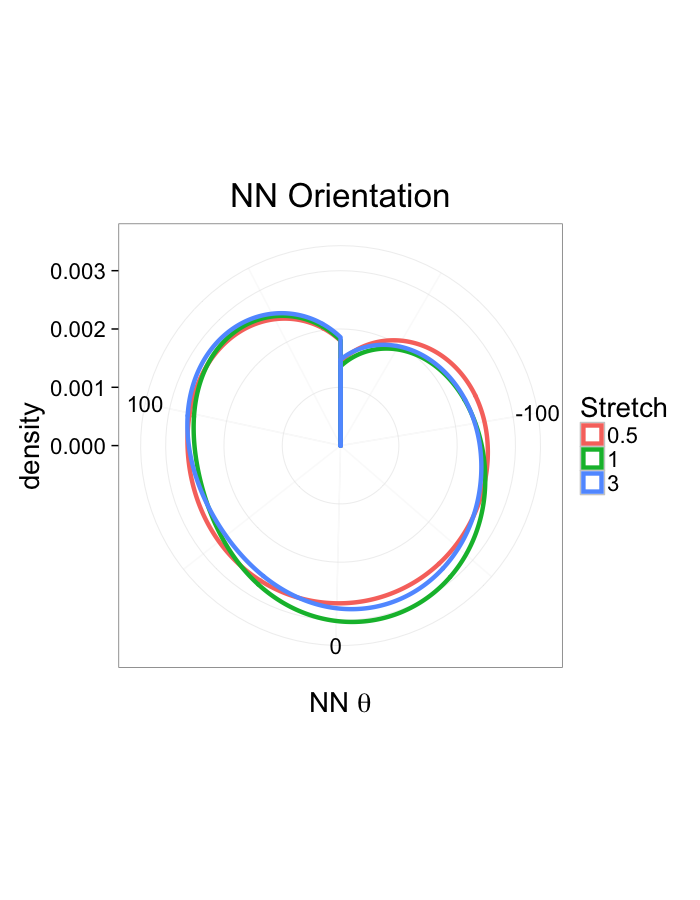
  theme_bw(20)

ggplot(dist.plots,      
       aes(x=180/pi*atan2(ye-y,xe-x),fill=as.factor(glab)))+
  geom_histogram(binwidth=45)+
    labs(x=expression(paste("NN ",theta)),title="NN Orientation",fill="Stretch")+
  scale_y_sqrt()+
  theme_bw(20)

Examining Swirl Systems

swirl.fun<-function(c.swirl,in.grid=cur.grid) {
  in.grid$cdist<-with(in.grid,sqrt(x^2+y^2))
  str.grid<-in.grid
  str.grid$x<-with(in.grid,cos(c.swirl*cdist)*x-sin(c.swirl*cdist)*y)
  str.grid$y<-with(in.grid,cos(c.swirl*cdist)*y+sin(c.swirl*cdist)*x)
  cbind(str.grid,glab=round(c.swirl*180/pi))
}

test.systems.swirl<-ldply(c(0,pi/40,pi/10),swirl.fun)

dist.plots.swirl<-ddply(test.systems.swirl,.(glab),find.nn)

ggplot(test.systems.swirl,aes(x=x,y=y))+
  geom_segment(data=dist.plots.swirl,aes(xend=xe,yend=ye),
               arrow=arrow(length = unit(0.3,"cm")),alpha=0.75)+
  geom_point(aes(color=val),size=3,alpha=0.75)+
  labs(title="Positions and Neighbors",color="Label")+
  scale_color_gradientn(colours=rainbow(10))+
    coord_equal()+
  facet_grid(glab~.)+
  theme_bw(20)+guides(color=F)

ggplot(dist.plots.swirl,
       aes(x=0,y=0,xend=xe-x,yend=ye-y))+
    geom_density2d(aes(x=xe-x,y=ye-y),color="red",alpha=0.7)+
  geom_segment(
               arrow=arrow(length = unit(0.3,"cm")))+
  facet_grid(glab~.)+
    coord_equal()+
  labs(title="Nearest Neighbor Orientations")+
  theme_bw(20)+guides(color=F)

Swirl NN Distributions

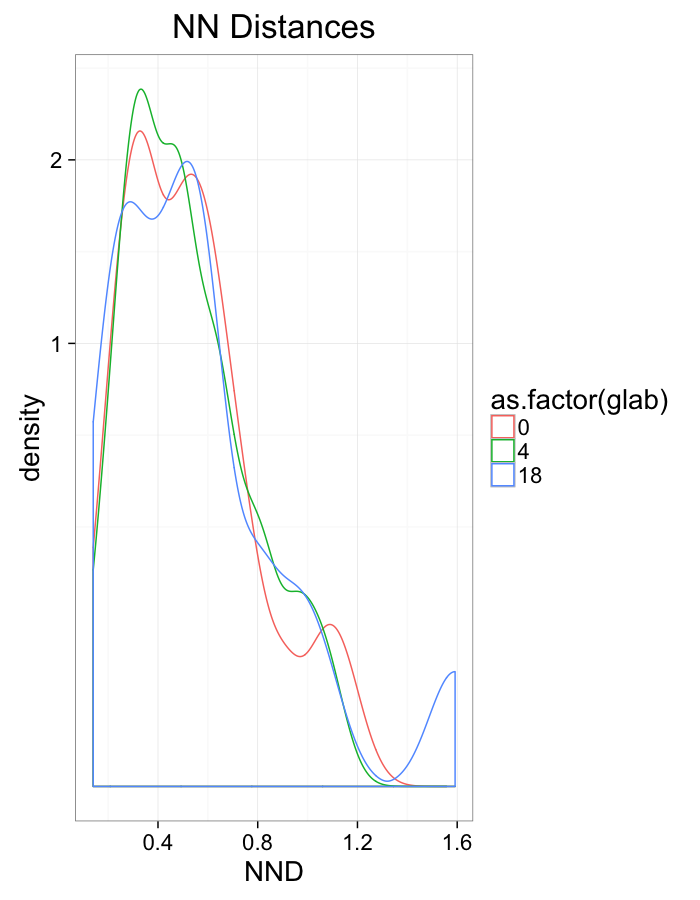
ggplot(dist.plots.swirl,      
       aes(x=dist,fill=as.factor(glab)))+
  geom_histogram(binwidth=0.25)+
  labs(x="NND",title="NN Distances",fill="Swirl")+
  scale_y_sqrt()+
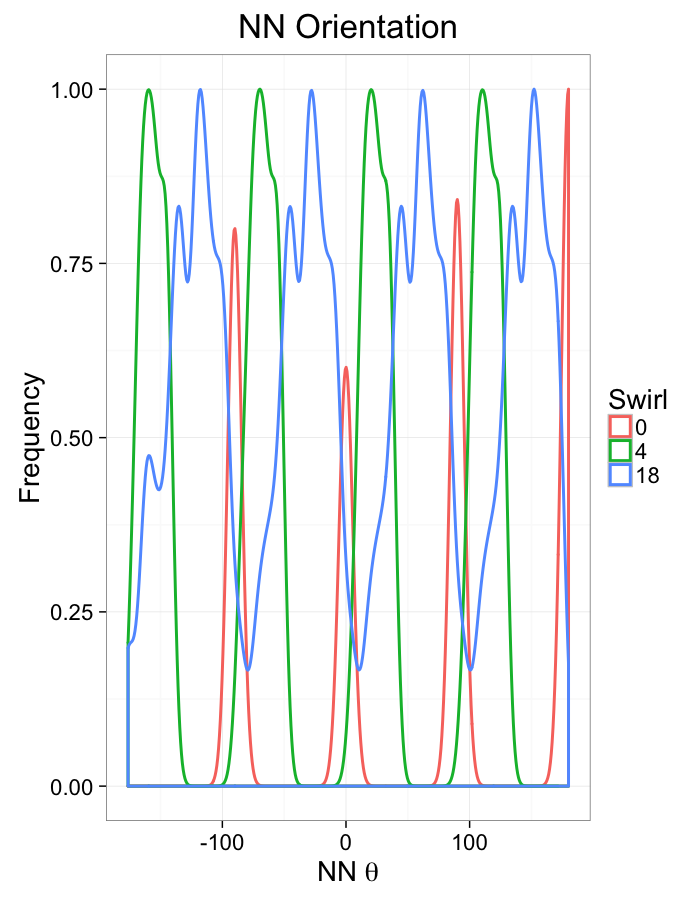
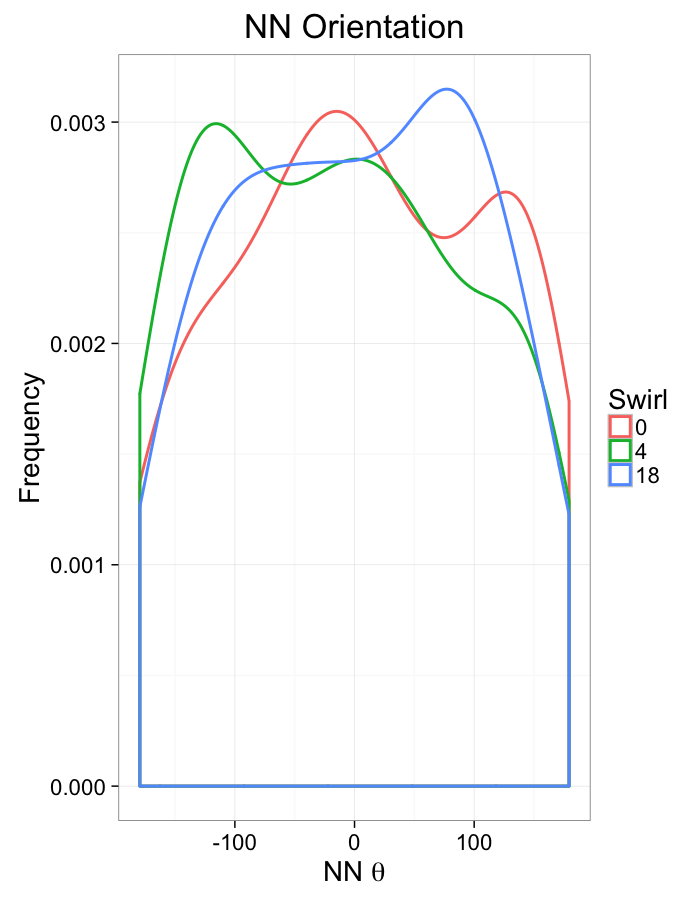
  theme_bw(20)

ggplot(dist.plots.swirl,      
       aes(x=180/pi*atan2(ye-y,xe-x),color=as.factor(glab)))+
  geom_density(aes(y=..scaled..),size=1,adjust=1/7)+
    labs(x=expression(paste("NN ",theta)),title="NN Orientation",color="Swirl",y="Frequency")+
  #scale_y_sqrt()+
  theme_bw(20)

What we notice

We notice there are several fairly significant short-comings of these metrics (particularly with in-silico systems)

Orientation appears to be useful but random

Why should it matter if one side is 0.01% closer?

Single outlier objects skew results
We only extract one piece of information
Difficult to create metrics

Fit a peak to the angle distribution and measure the width as the “angle variability”?

Luckily we are not the first people to address this issue

Random Systems

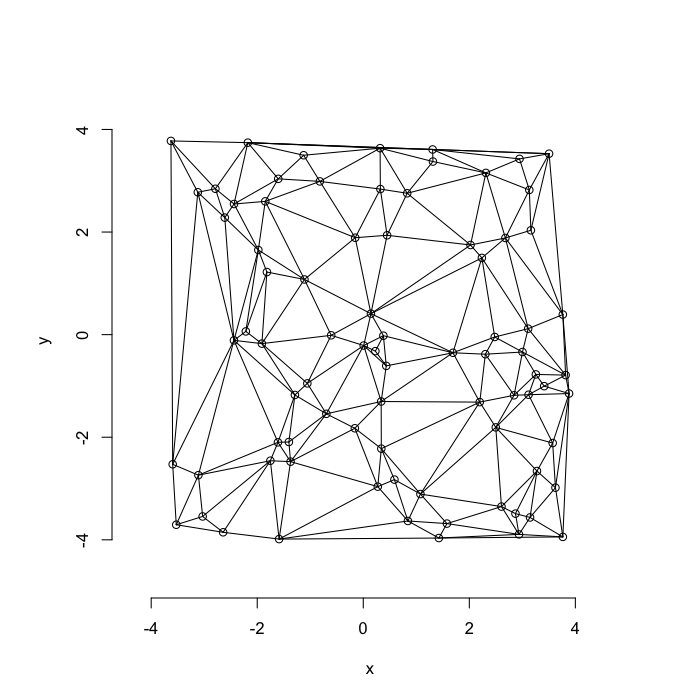
Using a uniform grid of points as a starting point has a strong influence on the results. A better approach is to use a randomly distributed series of points

resembles real data much better
avoids these symmetry problems
ϵ sized edges or overlaps
identical distances to nearby objects

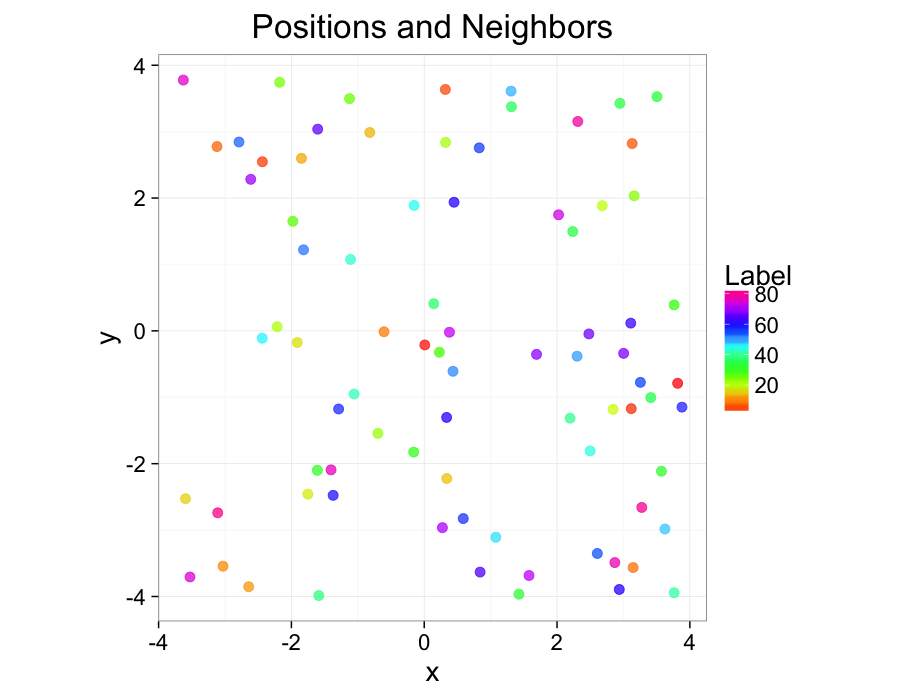
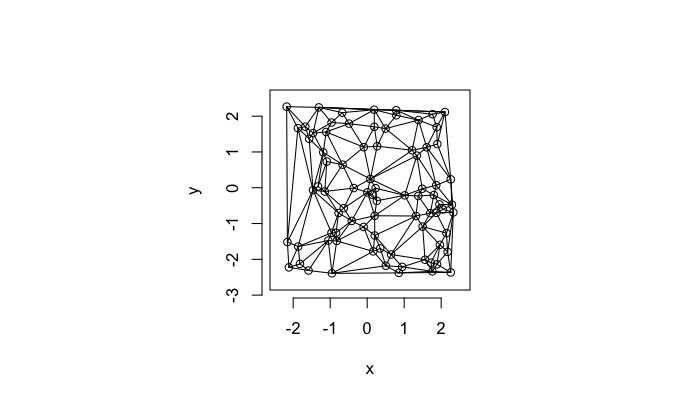
cur.grid<-data.frame(x=runif(81,min=-4,max=4),y=runif(81,min=-4,max=4))
cur.grid$val<-1:nrow(cur.grid)

ggplot(cur.grid,aes(x=x,y=y))+
  geom_point(aes(color=val),size=3,alpha=0.75)+
  labs(title="Positions and Neighbors",color="Label")+
  scale_color_gradientn(colours=rainbow(10))+
    coord_equal()+
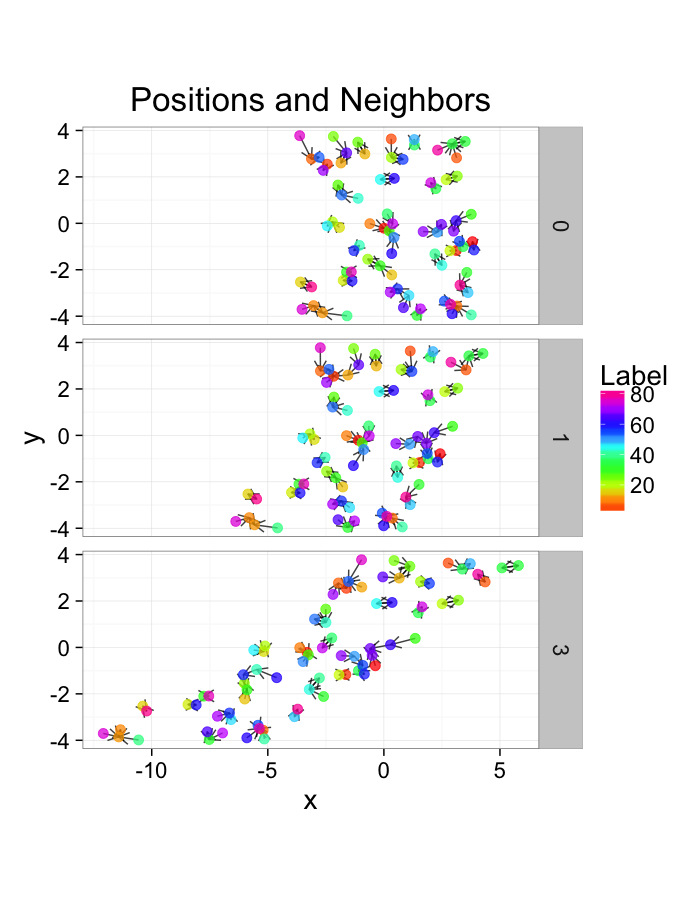
  theme_bw(20)

Examining Compression

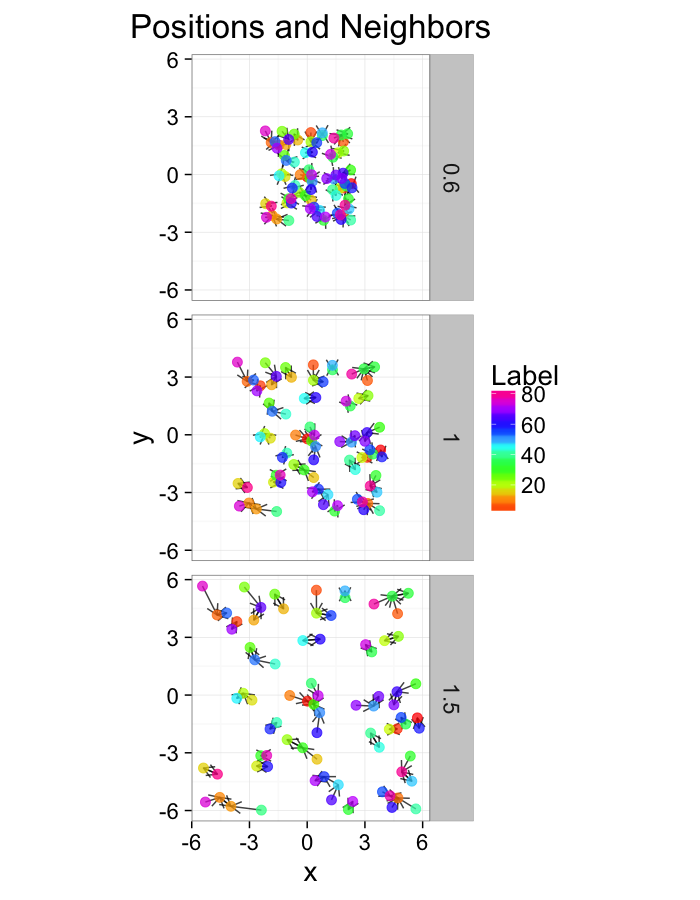
test.systems.comp<-ldply(c(0.6,1,1.5),function(c.stretch) {
  str.grid<-cur.grid
  str.grid$x<-with(cur.grid,c.stretch*x)
  str.grid$y<-with(cur.grid,c.stretch*y)
  cbind(str.grid,glab=c.stretch)
})

dist.plots.comp<-ddply(test.systems.comp,.(glab),find.nn)
ggplot(test.systems.comp,aes(x=x,y=y))+
  geom_segment(data=dist.plots.comp,aes(xend=xe,yend=ye),
               arrow=arrow(length = unit(0.3,"cm")),alpha=0.75)+
  geom_point(aes(color=val),size=3,alpha=0.75)+
  labs(title="Positions and Neighbors",color="Label")+
  scale_color_gradientn(colours=rainbow(10))+
    coord_equal()+
  facet_grid(glab~.)+
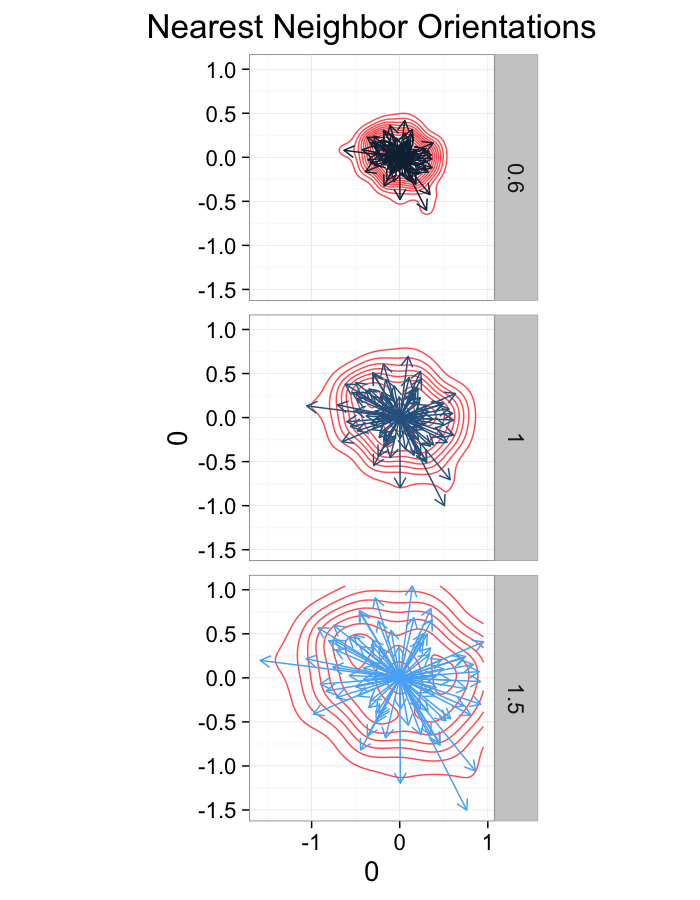
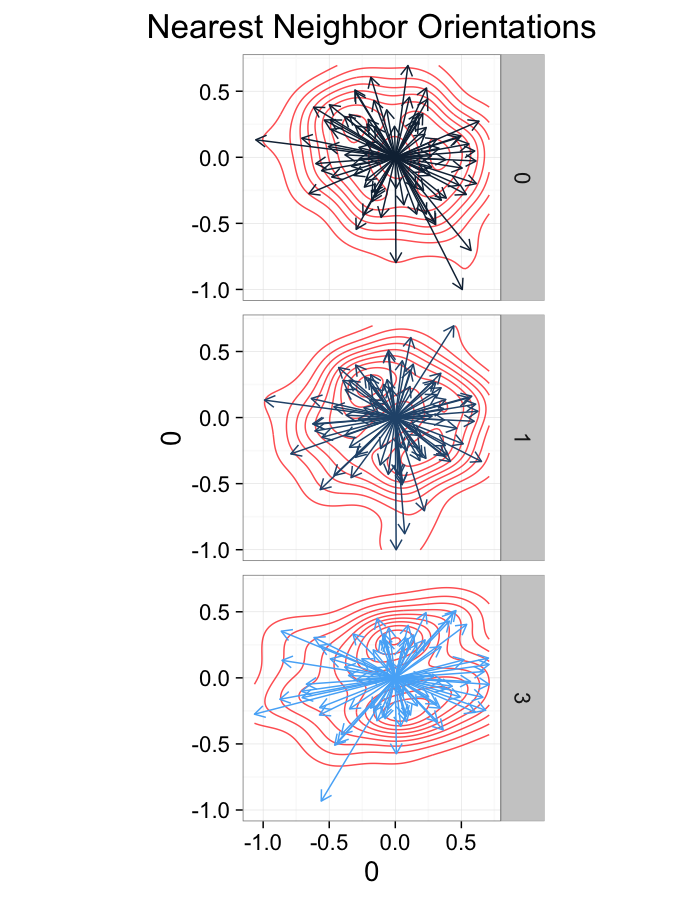
  theme_bw(20)

ggplot(dist.plots.comp,
       aes(x=0,y=0,xend=xe-x,yend=ye-y))+
    geom_density2d(aes(x=xe-x,y=ye-y),color="red",alpha=0.7)+
  geom_segment(aes(color=glab),
               arrow=arrow(length = unit(0.3,"cm")))+
  facet_grid(glab~.)+
    coord_equal()+
  labs(title="Nearest Neighbor Orientations")+guides(color=F)+
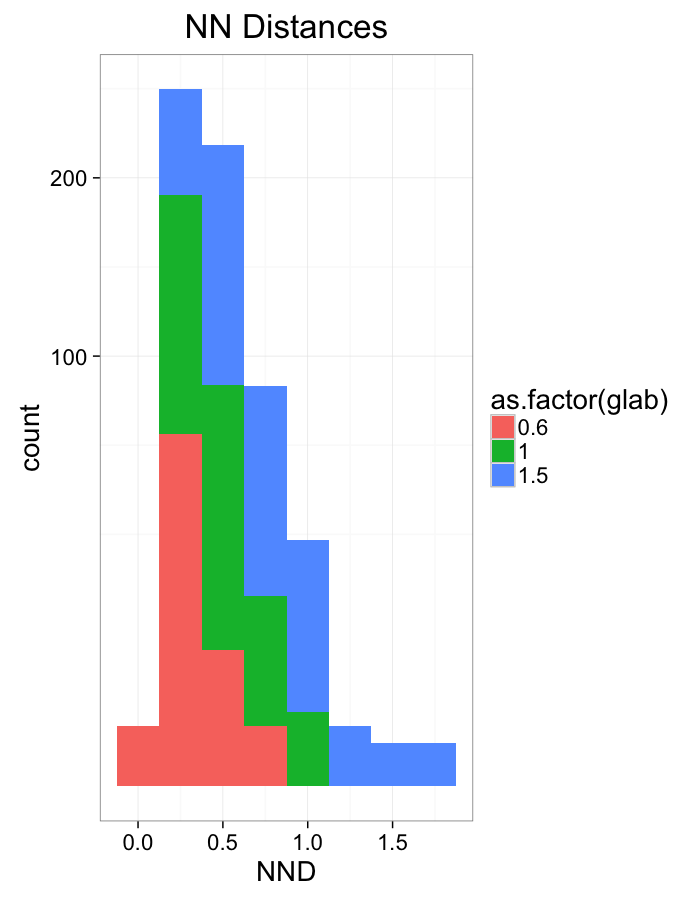
  theme_bw(20)

Compression Distributions

ggplot(dist.plots.comp,      
       aes(x=dist,fill=as.factor(glab)))+
  geom_histogram(binwidth=0.25)+
  labs(x="NND",title="NN Distances",color="Stretch")+
  scale_y_sqrt()+
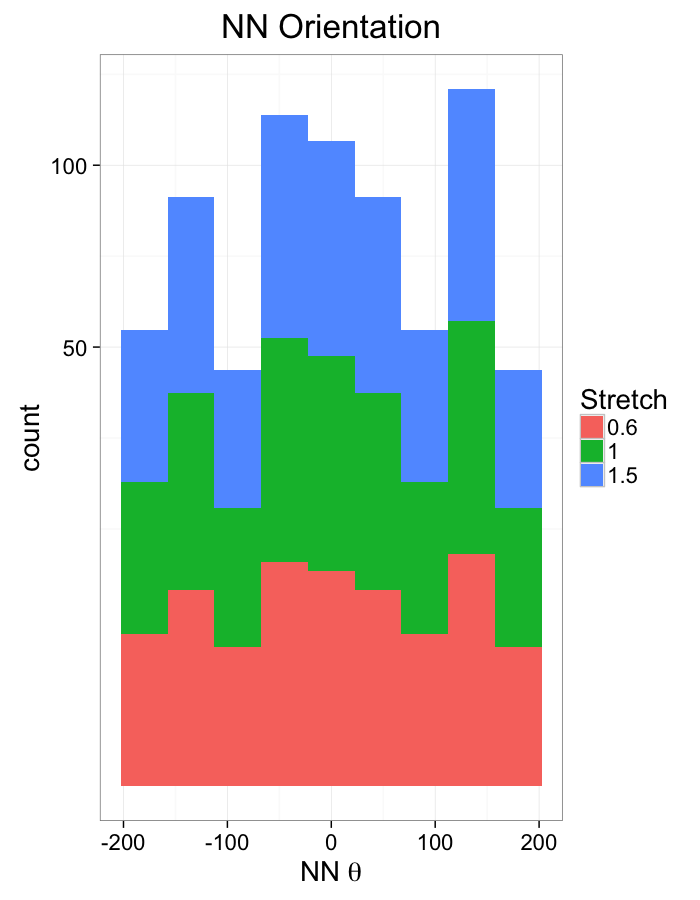
  theme_bw(20)

ggplot(dist.plots.comp,      
       aes(x=180/pi*atan2(ye-y,xe-x),fill=as.factor(glab)))+
  geom_histogram(binwidth=45)+
    labs(x=expression(paste("NN ",theta)),title="NN Orientation",fill="Stretch")+
  scale_y_sqrt()+
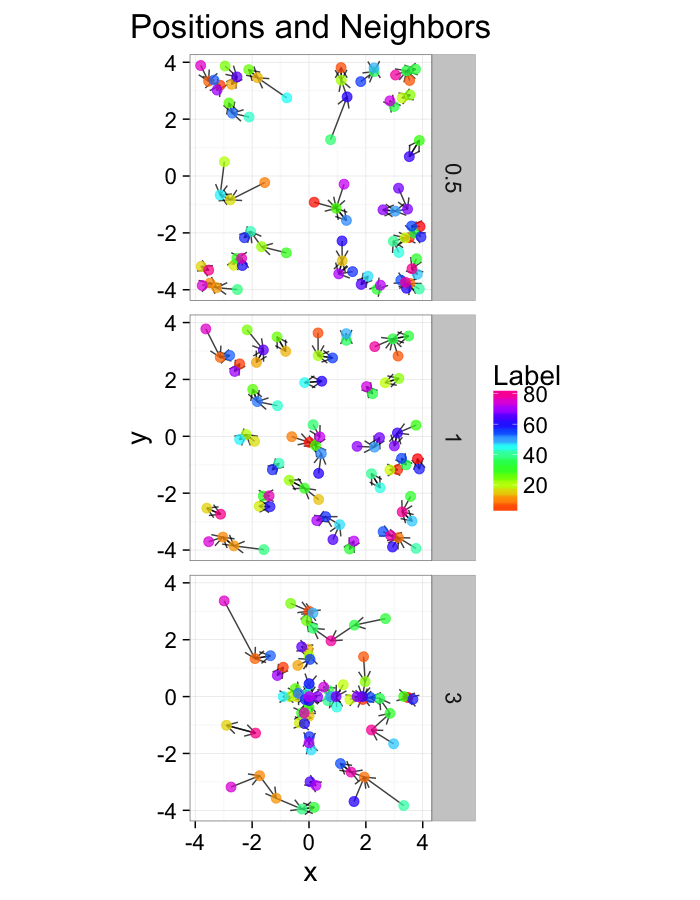
  theme_bw(20)

Examining Different Shears

test.systems.shear<-ldply(c(0,1,3),function(c.shear) {
  str.grid<-cur.grid
  str.grid$x<-with(cur.grid,x+c.shear*(y-2)/2)
  cbind(str.grid,glab=c.shear)
})

dist.plots.shear<-ddply(test.systems.shear,.(glab),find.nn)
ggplot(test.systems.shear,aes(x=x,y=y))+
  geom_segment(data=dist.plots.shear,aes(xend=xe,yend=ye),
               arrow=arrow(length = unit(0.3,"cm")),alpha=0.75)+
  geom_point(aes(color=val),size=3,alpha=0.75)+
  labs(title="Positions and Neighbors",color="Label")+
  scale_color_gradientn(colours=rainbow(10))+
    coord_equal()+
  facet_grid(glab~.)+
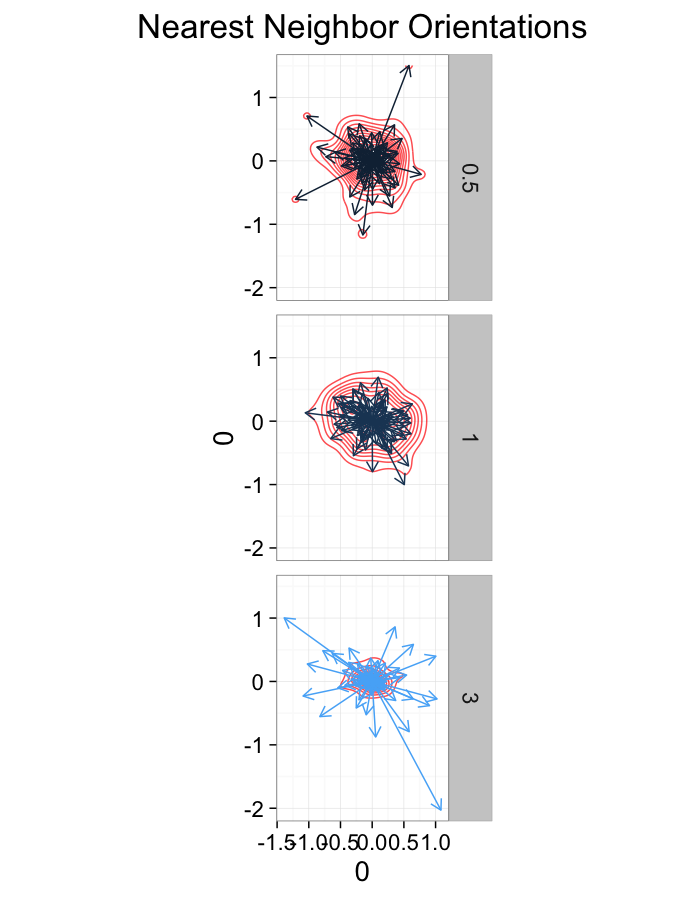
  theme_bw(20)

ggplot(dist.plots.shear,
       aes(x=0,y=0,xend=xe-x,yend=ye-y))+
  geom_density2d(aes(x=xe-x,y=ye-y),color="red",alpha=0.7)+
  geom_segment(aes(color=glab),
               arrow=arrow(length = unit(0.3,"cm")))+
  facet_grid(glab~.)+
    coord_equal()+
  labs(title="Nearest Neighbor Orientations")+guides(color=F)+
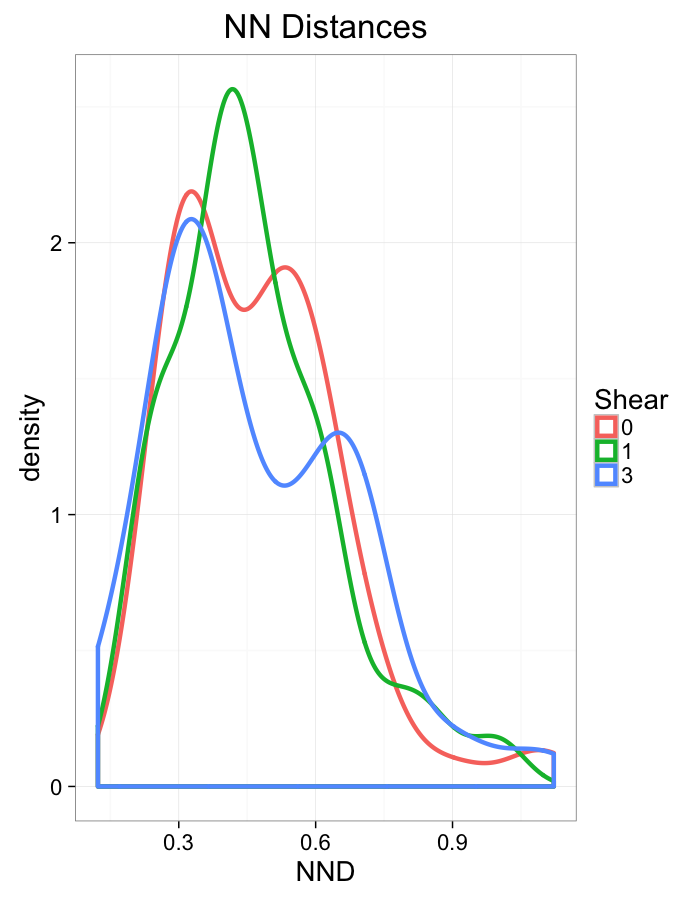
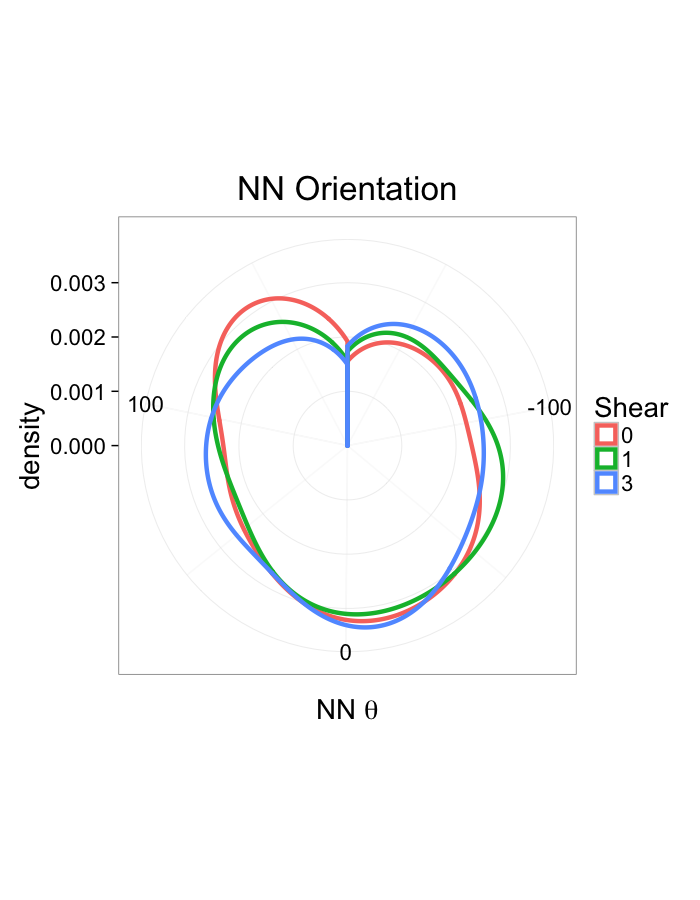
  theme_bw(20)

Shear Distributions

ggplot(dist.plots.shear,      
       aes(x=dist,color=as.factor(glab)))+
  geom_density(size=1.5,adjust=1)+
  labs(x="NND",title="NN Distances",color="Shear")+
  theme_bw(20)

ggplot(dist.plots.shear,      
       aes(x=180/pi*atan2(ye-y,xe-x),color=as.factor(glab)))+
  geom_density(size=1.5,adjust=1/1.5)+
    labs(x=expression(paste("NN ",theta)),title="NN Orientation",color="Shear")+
  coord_polar()+
  theme_bw(20)

Examining Different Stretches

str.fun<-function(x,a=1,r=4) sign(x)*r*(abs(x)/r)^a
test.systems<-ldply(c(0.5,1,3),function(c.stretch) {
  str.grid<-cur.grid
  str.grid$x<-with(cur.grid,str.fun(x,a=c.stretch))
  str.grid$y<-with(cur.grid,str.fun(y,a=c.stretch))
  cbind(str.grid,glab=c.stretch)
})

dist.plots<-ddply(test.systems,.(glab),find.nn)
ggplot(test.systems,aes(x=x,y=y))+
  geom_segment(data=dist.plots,aes(xend=xe,yend=ye),
               arrow=arrow(length = unit(0.3,"cm")),alpha=0.75)+
  geom_point(aes(color=val),size=3,alpha=0.75)+
  labs(title="Positions and Neighbors",color="Label")+
  scale_color_gradientn(colours=rainbow(10))+
    coord_equal()+
  facet_grid(glab~.)+
  theme_bw(20)

ggplot(dist.plots,
       aes(x=0,y=0,xend=xe-x,yend=ye-y))+
    geom_density2d(aes(x=xe-x,y=ye-y),color="red",alpha=0.7)+
  geom_segment(aes(color=glab),
               arrow=arrow(length = unit(0.3,"cm")))+
  facet_grid(glab~.)+
    coord_equal()+
  labs(title="Nearest Neighbor Orientations")+guides(color=F)+
  theme_bw(20)

Stretch Distributions

ggplot(dist.plots,      
       aes(x=dist,color=as.factor(glab)))+
  geom_density(size=1.5,adjust=1)+
  #geom_histogram(binwidth=0.25)+
  labs(x="NND",title="NN Distances",color="Stretch")+
  theme_bw(20)

ggplot(dist.plots,      
       aes(x=180/pi*atan2(ye-y,xe-x),color=as.factor(glab)))+
  #geom_histogram(binwidth=45)+
  geom_density(size=1.5,adjust=1)+
    labs(x=expression(paste("NN ",theta)),title="NN Orientation",color="Stretch")+
  coord_polar()+
  theme_bw(20)

Examining Swirl Systems

cur.grid$cdist<-with(cur.grid,sqrt(x^2+y^2))
test.systems.swirl<-ldply(c(0,pi/40,pi/10),function(c.swirl) {
  str.grid<-cur.grid
  str.grid$x<-with(cur.grid,cos(c.swirl*cdist)*x-sin(c.swirl*cdist)*y)
  str.grid$y<-with(cur.grid,cos(c.swirl*cdist)*y+sin(c.swirl*cdist)*x)
  cbind(str.grid,glab=round(c.swirl*180/pi))
})

dist.plots.swirl<-ddply(test.systems.swirl,.(glab),find.nn)

ggplot(test.systems.swirl,aes(x=x,y=y))+
  geom_segment(data=dist.plots.swirl,aes(xend=xe,yend=ye),
               arrow=arrow(length = unit(0.3,"cm")),alpha=0.75)+
  geom_point(aes(color=val),size=3,alpha=0.75)+
  labs(title="Positions and Neighbors",color="Label")+
  scale_color_gradientn(colours=rainbow(10))+
    coord_equal()+
  facet_grid(glab~.)+
  theme_bw(20)+guides(fill=F)

ggplot(dist.plots.swirl,
       aes(x=0,y=0,xend=xe-x,yend=ye-y))+
    geom_density2d(aes(x=xe-x,y=ye-y),color="red",alpha=0.7)+
  geom_segment(aes(color=glab),
               arrow=arrow(length = unit(0.3,"cm")))+
  facet_grid(glab~.)+
    coord_equal()+
  labs(title="Nearest Neighbor Orientations")+
  theme_bw(20)

Swirl NN Distributions

ggplot(dist.plots.swirl,      
       aes(x=dist,color=as.factor(glab)))+
  geom_density()+
  labs(x="NND",title="NN Distances",fill="Swirl")+
  scale_y_sqrt()+
  theme_bw(20)

ggplot(dist.plots.swirl,      
       aes(x=180/pi*atan2(ye-y,xe-x),color=as.factor(glab)))+
  geom_density(size=1,adjust=1)+
    labs(x=expression(paste("NN ",theta)),title="NN Orientation",color="Swirl",y="Frequency")+
  #scale_y_sqrt()+
  theme_bw(20)

Voronoi Tesselation

library(deldir)
dd.grid.summary<-function(c.grid,...) {
  c.dd<-deldir(c.grid,...)
  c.vor<-c.dd$dirsgs
  n.pts<-as.vector(summary(as.factor(c(c.vor$ind1,c.vor$ind2))))
  n.vec<-data.frame(ind=1:length(n.pts),
                    n.count=n.pts,
                    area=c.dd$summary$dir.area)
  merge(c.grid,n.vec,by.x="val",by.y="ind")
}
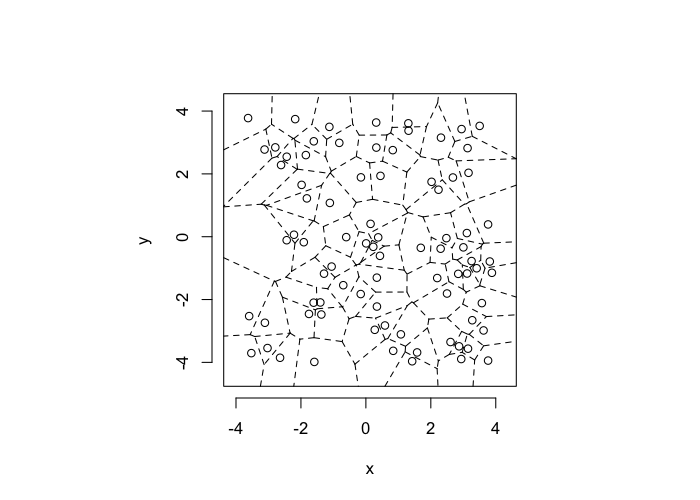
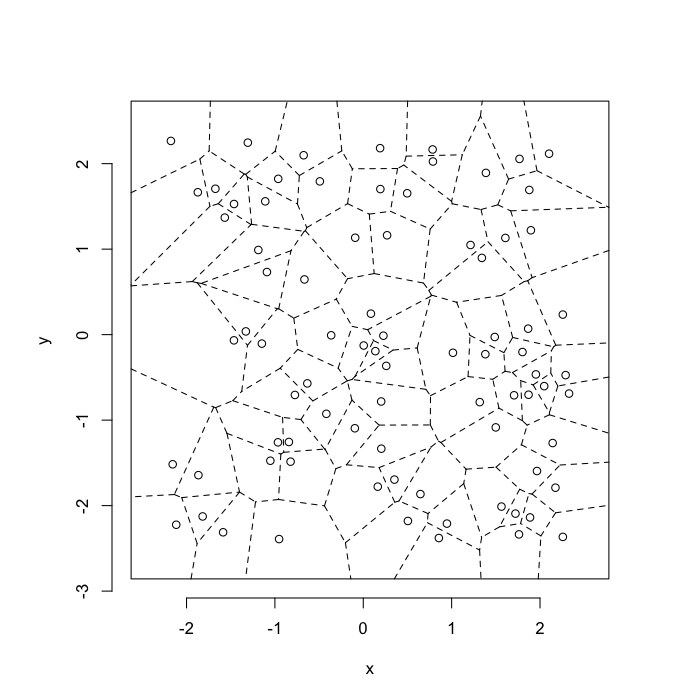
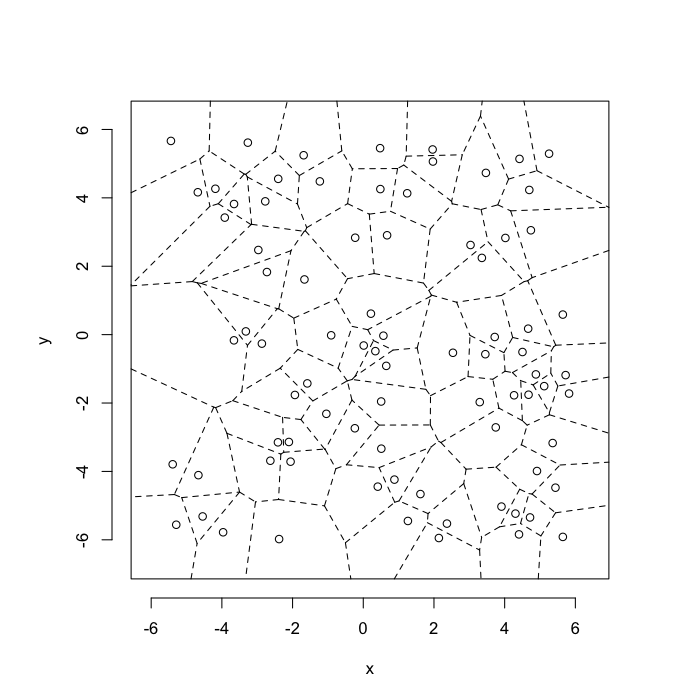
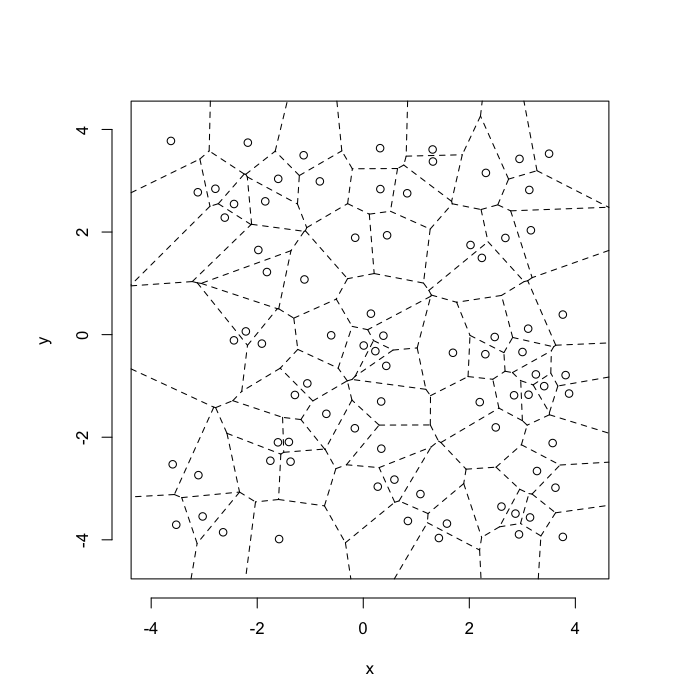
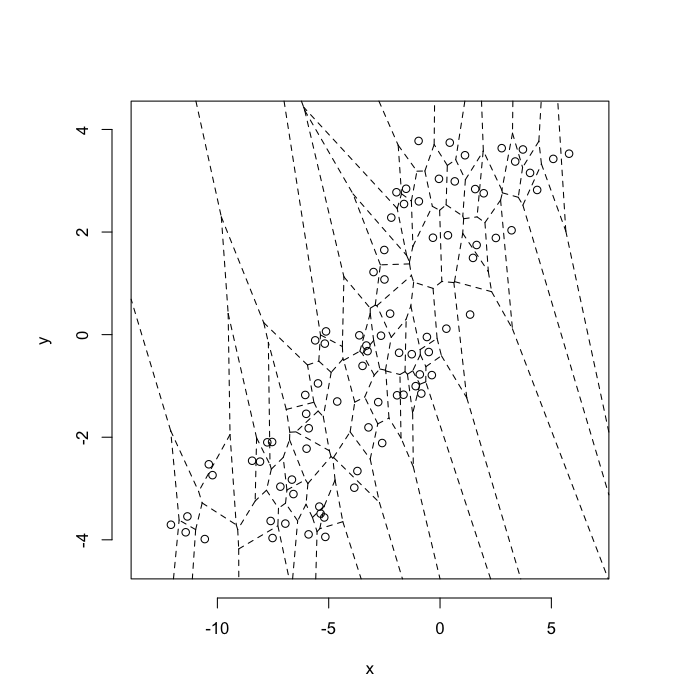
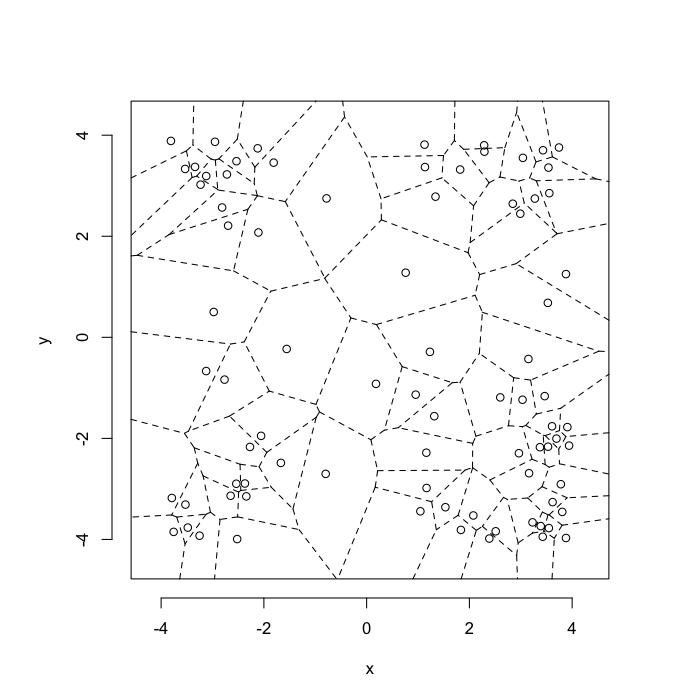
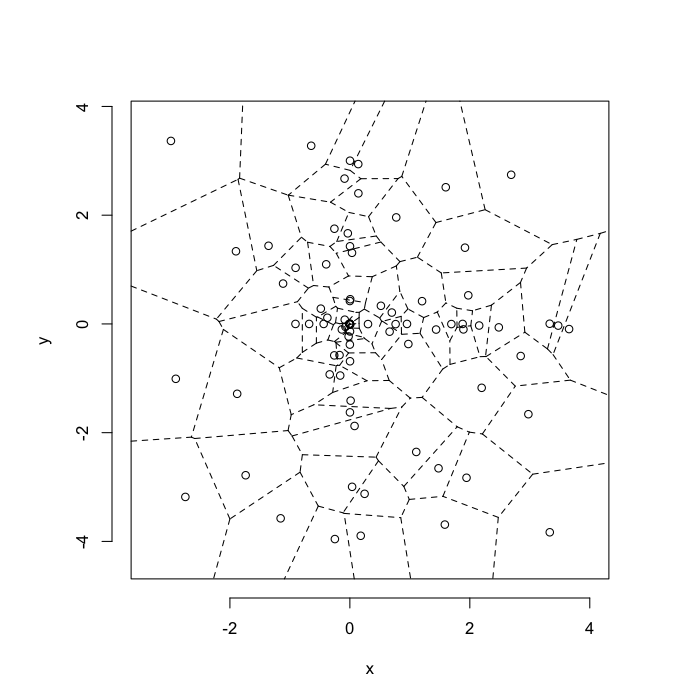
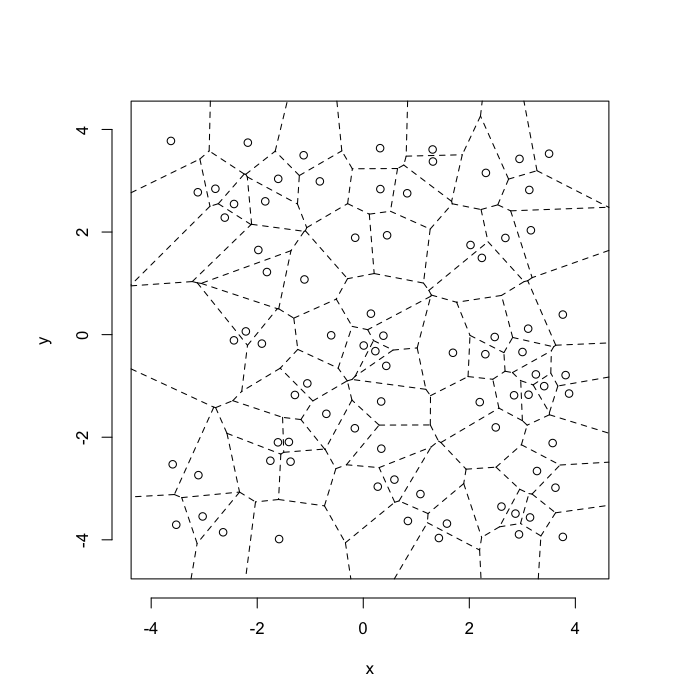
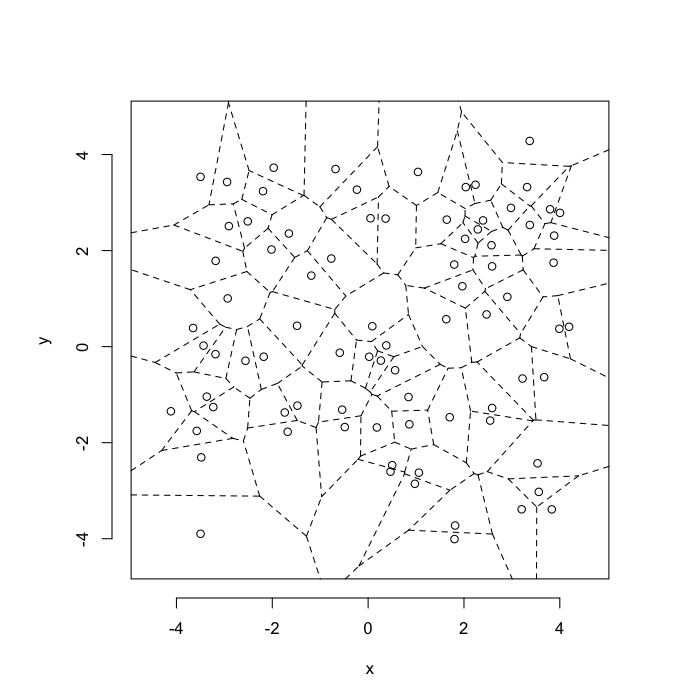
dd.summary<-function(in.df) ddply(in.df,.(glab),dd.grid.summary)

Voronoi tesselation is a method for partitioning a space based on points. The basic idea is that each point $\vec{p}$ is assigned a region R consisting of points which are closer to $\vec{p}$ than any of the other points. Below the diagram is shown in a dashed line for the points shown as small circles.

plot(deldir(std.grid),wlines=c('tess'),showrect=T)

We call the area of a region (R) around point $\vec{p}$ its territory.

The grid on the random system, shows much more diversity in territory area.

plot(deldir(cur.grid),wlines=c('tess'),showrect=T)

Calculating Density

Back to our original density problem of having just one number to broadly describe the system.

Can a voronoi tesselation help us with this?
YES

With density we calculated

$\textrm{Density} = \frac{\textrm{Number of Objects}}{\textrm{Total Volume}}$
with the regions we have a territory (volume) per object so the average territory is
$\bar{Territory} = \frac{\sum \textrm{Territory}_i}{\textrm{Number of Objects}} = \frac{\textrm{Total Volume}}{\textrm{Number of Objects}} = \frac{1}{\textrm{Density}}$
So the same, but we now have a density definition for a single point!
$\textrm{Density}_i = \frac{1}{\textrm{Territory}_i}$

Density Examples

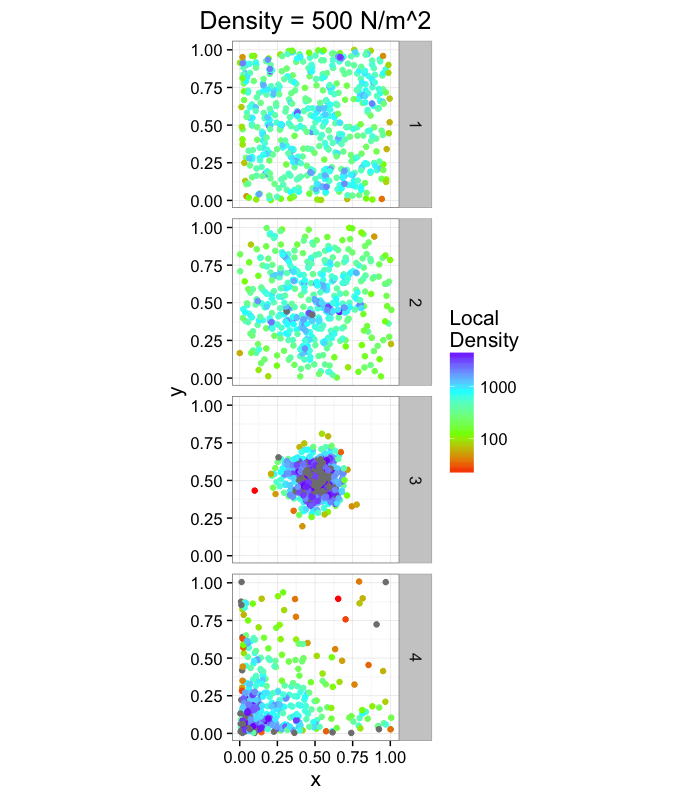
rand.pnts<-ldply(1:length(dist.funs),function(fun.ind) {
  out.pts<-pt.maker(500,rn.fun=dist.funs[[fun.ind]],fun.ind=fun.ind)
  out.pts$val<-1:nrow(out.pts)
  out.pts
})
ggplot(ddply(rand.pnts,.(fun.ind),function(in.pts) deldir(in.pts)$summary),
       aes(x,y,color=1/dir.area))+
  geom_point()+facet_grid(fun.ind~.)+
  scale_color_gradientn(colours=rainbow(4),trans="log10",limits=c(20,5000))+
  coord_equal()+
  xlim(0,1.01)+ylim(0,1.01)+
  labs(title="Density = 500 N/m^2",color="Local\nDensity")+
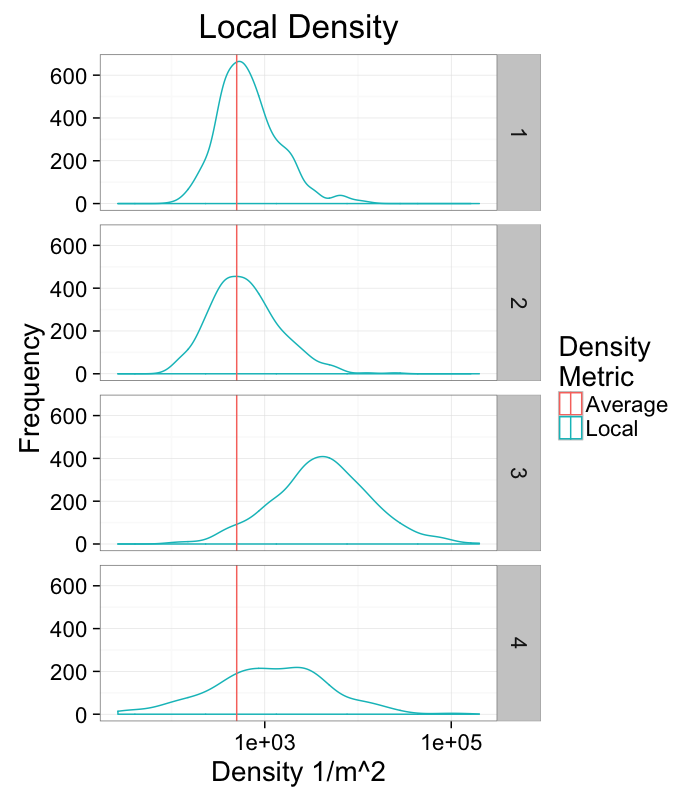
  theme_bw(15)

ggplot(cbind(ddply(rand.pnts,.(fun.ind),function(c.block) deldir(c.block,rw=c(0,1,0,1))$summary),mn.pos=500),                 
       aes(x=1/del.area))+
  geom_density(aes(y=..count..,color="Local"))+
  geom_vline(aes(colour="Average",xintercept=mn.pos))+
  facet_grid(fun.ind~.)+
  scale_x_log10()+
  labs(title="Local Density",x="Density 1/m^2",y="Frequency",color="Density\nMetric")+
  theme_bw(20)

Delaunay Triangulation

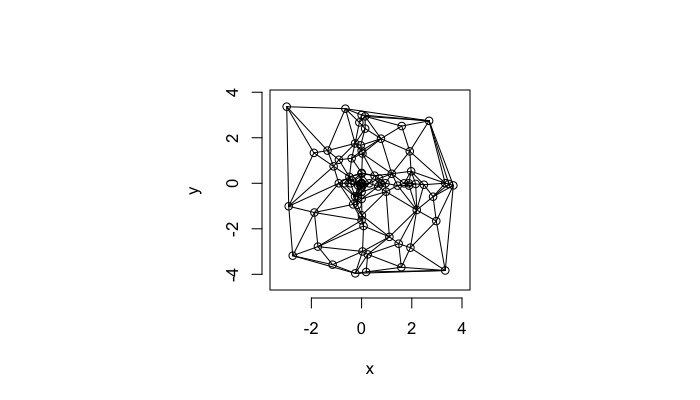
A parallel or dual idea where triangles are used and each triangle is created such that the circle which encloses it contains no other points. The triangulation makes the neighbors explicit since connected points in the triangulation correspond to points in our tesselation which share an edge (or face in 3D)

plot(deldir(std.grid),wlines=c('triang'))

We define the number of connections each point $\vec{p}$ has the Neighbor Count or Delaunay Neighbor Count.

The triangulation on a random system has a much higher diversity in neighbor count

plot(deldir(cur.grid),wlines=c('triang'))

Compression System

Compression

v.comp<-quantile(test.systems.comp$glab,0.2)
plot(deldir(subset(test.systems.comp,glab==v.comp)),wlines=c('tess'),showrect=T)

Tension

v.comp<-quantile(test.systems.comp$glab,0.95)
plot(deldir(subset(test.systems.comp,glab==v.comp)),wlines=c('tess'),showrect=T)

Shear System

Low Shear

v.shear<-min(test.systems.shear$glab)
plot(deldir(subset(test.systems.shear,glab==v.shear)),wlines=c('tess'),showrect=T)

High Shear

v.shear<-max(test.systems.shear$glab)
plot(deldir(subset(test.systems.shear,glab==v.shear)),wlines=c('tess'),showrect=T)

Stretch System

Low Stretch

v.stretch<-min(test.systems$glab)
plot(deldir(subset(test.systems,glab==v.stretch)),wlines=c('tess'),showrect=T)

Highly Stretched System

v.stretch<-quantile(test.systems$glab,0.95)
plot(deldir(subset(test.systems,glab>=v.stretch)),wlines=c('tess'),showrect=T)

Swirl System

Low Swirl System

v.swirl<-min(test.systems.swirl$glab)
plot(deldir(subset(test.systems.swirl,glab==v.swirl)),wlines=c('tess'),showrect=T)

High Swirl System

v.swirl<-max(test.systems.swirl$glab)
plot(deldir(subset(test.systems.swirl,glab==v.swirl)),wlines=c('tess'),showrect=T)

Neighborhoods

Compression

v.comp<-min(test.systems.comp$glab)
plot(deldir(subset(test.systems.comp,glab==v.comp)),wlines=c('triang'),showrect=T)

Stretch

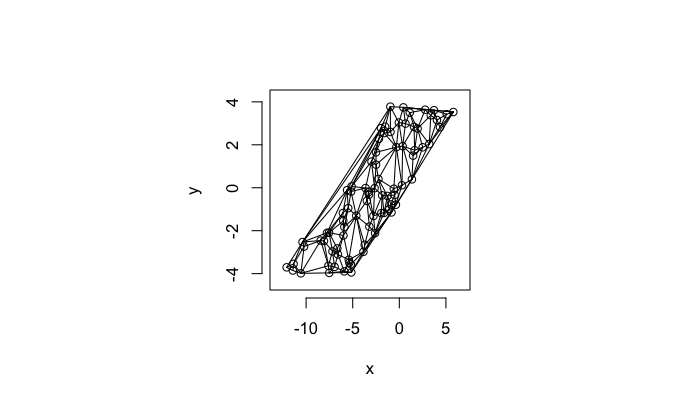
v.stretch<-max(test.systems$glab)
plot(deldir(subset(test.systems,glab==v.stretch)),wlines=c('triang'),showrect=T)

Shear

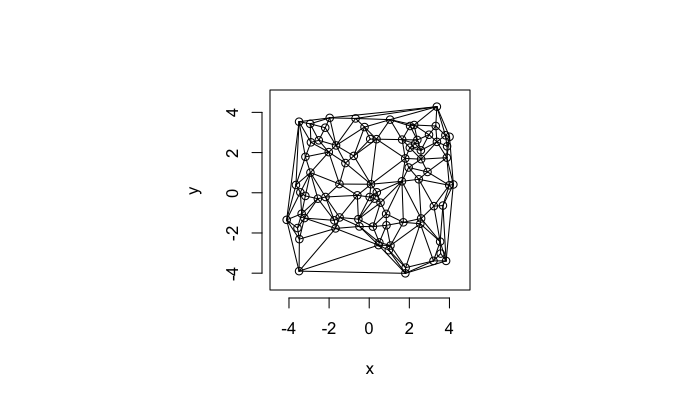
v.shear<-max(test.systems.shear$glab)
plot(deldir(subset(test.systems.shear,glab==v.shear)),wlines=c('triang'),showrect=T)

Swirl

v.stretch<-quantile(test.systems.swirl$glab,0.95)
plot(deldir(subset(test.systems.swirl,glab==v.stretch)),wlines=c('triang'),showrect=T)

Neighbor Count

test.systems.comp.vor<-dd.summary(test.systems.comp)
test.systems.vor<-dd.summary(test.systems)
test.systems.shear.vor<-dd.summary(test.systems.shear)
test.systems.swirl.vor<-dd.summary(test.systems.swirl)
test.all.vor<-rbind(cbind(test.systems.comp.vor,system="Compression",cdist=0),
      cbind(test.systems.vor,system="Stretching",cdist=0),
      cbind(test.systems.shear.vor,system="Shearing",cdist=0),
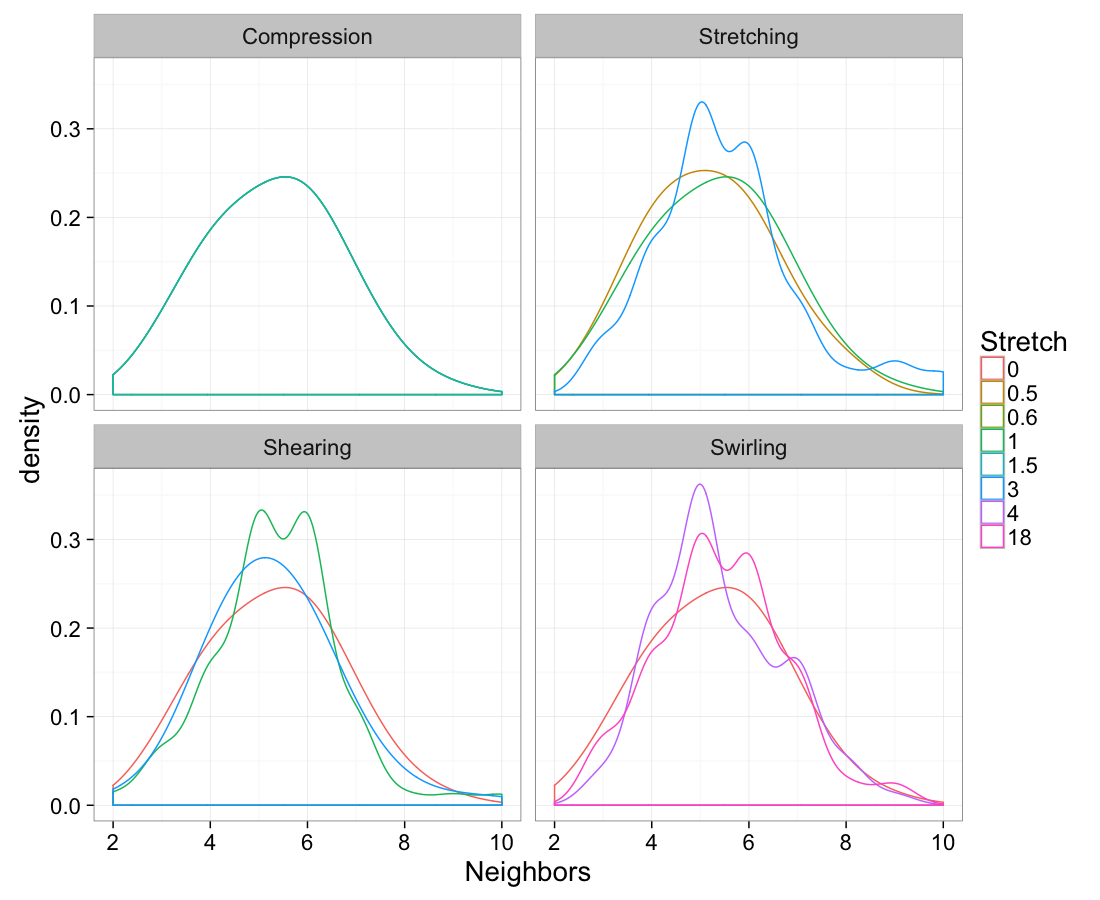
      cbind(test.systems.swirl.vor,system="Swirling"))

ggplot(test.all.vor,      
       aes(x=n.count))+
  geom_density(aes(color=as.factor(glab)),adjust=1.5)+
  labs(x="Neighbors",color="Stretch")+
  facet_wrap(~system)+
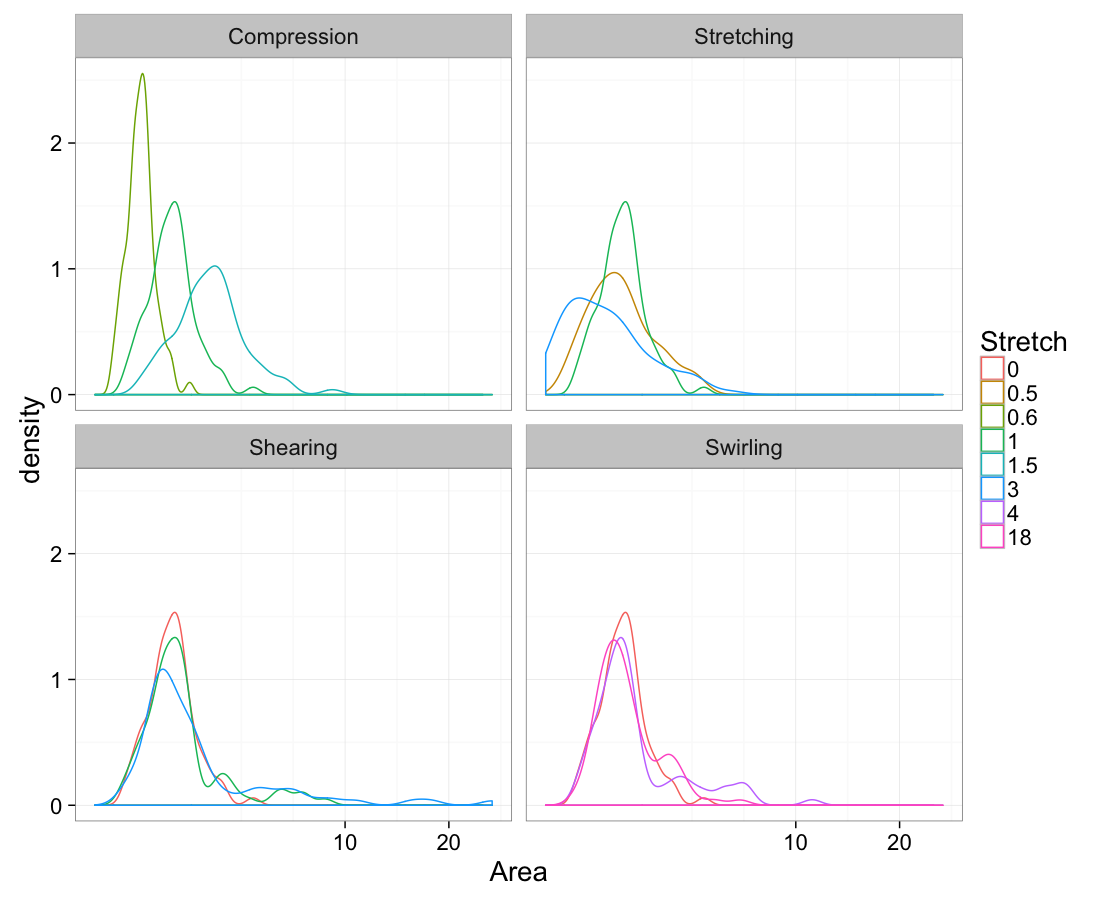
  theme_bw(20)

Volume

ggplot(test.all.vor,      
       aes(x=area))+
  geom_density(aes(color=as.factor(glab)))+
  labs(x="Area",color="Stretch")+
  facet_wrap(~system)+
  scale_x_sqrt()+
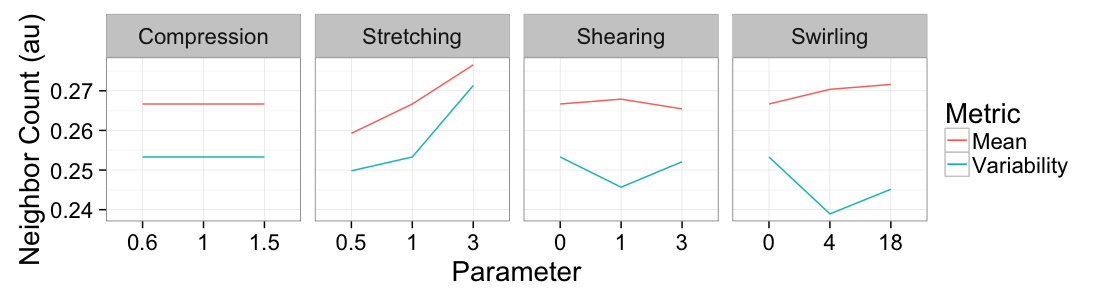
  theme_bw(20)

Mean vs Variability

ggplot(
  ddply(test.all.vor,.(glab,system),
        function(in.seg) with(in.seg,data.frame(mean.val=mean(n.count),std.val=sd(n.count)))),
  aes(x=as.factor(glab)))+
  geom_line(aes(y=mean.val/20,color="Mean",group=system))+  
  geom_line(aes(y=std.val/mean.val,color="Variability",group=system))+
  facet_grid(~system,scales="free_x")+
  labs(x="Parameter",y="Neighbor Count (au)",color="Metric")+
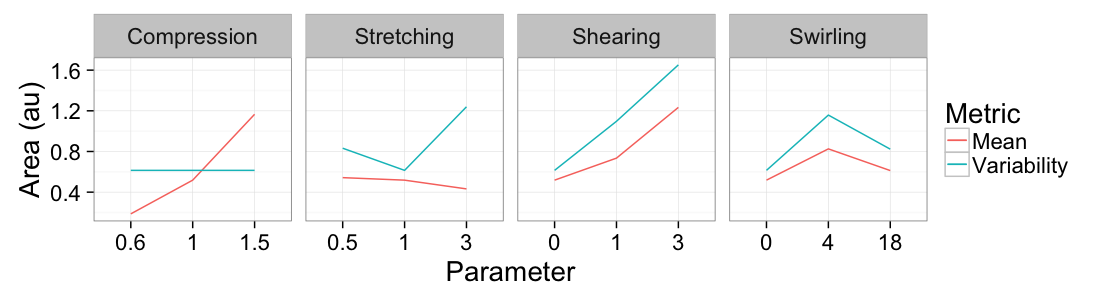
  theme_bw(20)

ggplot(
  ddply(test.all.vor,.(glab,system),
        function(in.seg) with(in.seg,data.frame(mean.val=mean(area),std.val=sd(area)))),
  aes(x=as.factor(glab)))+
  geom_line(aes(y=mean.val/2,color="Mean",group=system))+  
  geom_line(aes(y=std.val/mean.val,color="Variability",group=system))+
  facet_grid(~system,scales="free_x")+
  labs(x="Parameter",y="Area (au)",color="Metric")+
  theme_bw(20)

Where are we at?

We have introduced a number of “operations” we can perform on our objects to change their positions

compression
stretching
shearing
swirling

We have introduced a number of metrics to characterize our images

Nearest Neighbor distance
Nearest Neighbor angle
Delaunay Neighbor count
Territory Area (Volume)

A single random systems is useful

but in order to have a reasonable understanding of the behavior of a system we need to sample many of them.

Understand metrics as a random system + a known transformation

We take mean values
Also coefficient of variation (CV) values since they are “scale-free”

m.grid<-function(n.pts=81) {
  out.grid<-data.frame(x=runif(n.pts,min=-4,max=4),y=runif(n.pts,min=-4,max=4))
  out.grid$val<-1:nrow(out.grid)
  out.grid
}
all.metrics<-function(in.grid) {
  nn.df<-find.nn(in.grid)
  vor.df<-dd.grid.summary(in.grid)
  data.frame(NND=mean(nn.df$dist),
             NNTheta=mean(with(nn.df,180/pi*atan2(ye-y,xe-x))),
             DNC=mean(vor.df$n.count),
             Region.Ter=mean(vor.df$area),
             CV.NND=sd(nn.df$dist)/mean(nn.df$dist),
             SD.NNTheta=sd(with(nn.df,180/pi*atan2(ye-y,xe-x))),
             CV.DNC=sd(vor.df$n.count)/mean(vor.df$n.count),
             CV.Region.Ter=sd(vor.df$area)/mean(vor.df$area)
             )
}

many.grid<-function(n.grid,n.pts=81,trans.fun=function(in.pts) in.pts) {
  ldply(1:n.grid,function(n) {
    s.grid<-trans.fun(m.grid(n.pts))
    all.metrics(s.grid)
  },.parallel=T)
}
c.pts<-20

Understanding Metrics

In imaging science we always end up with lots of data, the tricky part is understanding the results that come out. With this simulation-based approach

we generate completely random data
apply a known transformation to it ℱ
quantify the results

We can then take this knowledge and use it to interpret observed data as transformations on an initially random system. We try and find the rules used to produce the sample

Examples

Cell distribution in bone

Cell position appears random
Metrics ≠ Random Statistics
Cells are consistently self-avoiding or stretched

Egg-shell Pores

Pores in rock / egg shell appear random
Metrics ≠ Random Statistics
Pores are also self-avoiding

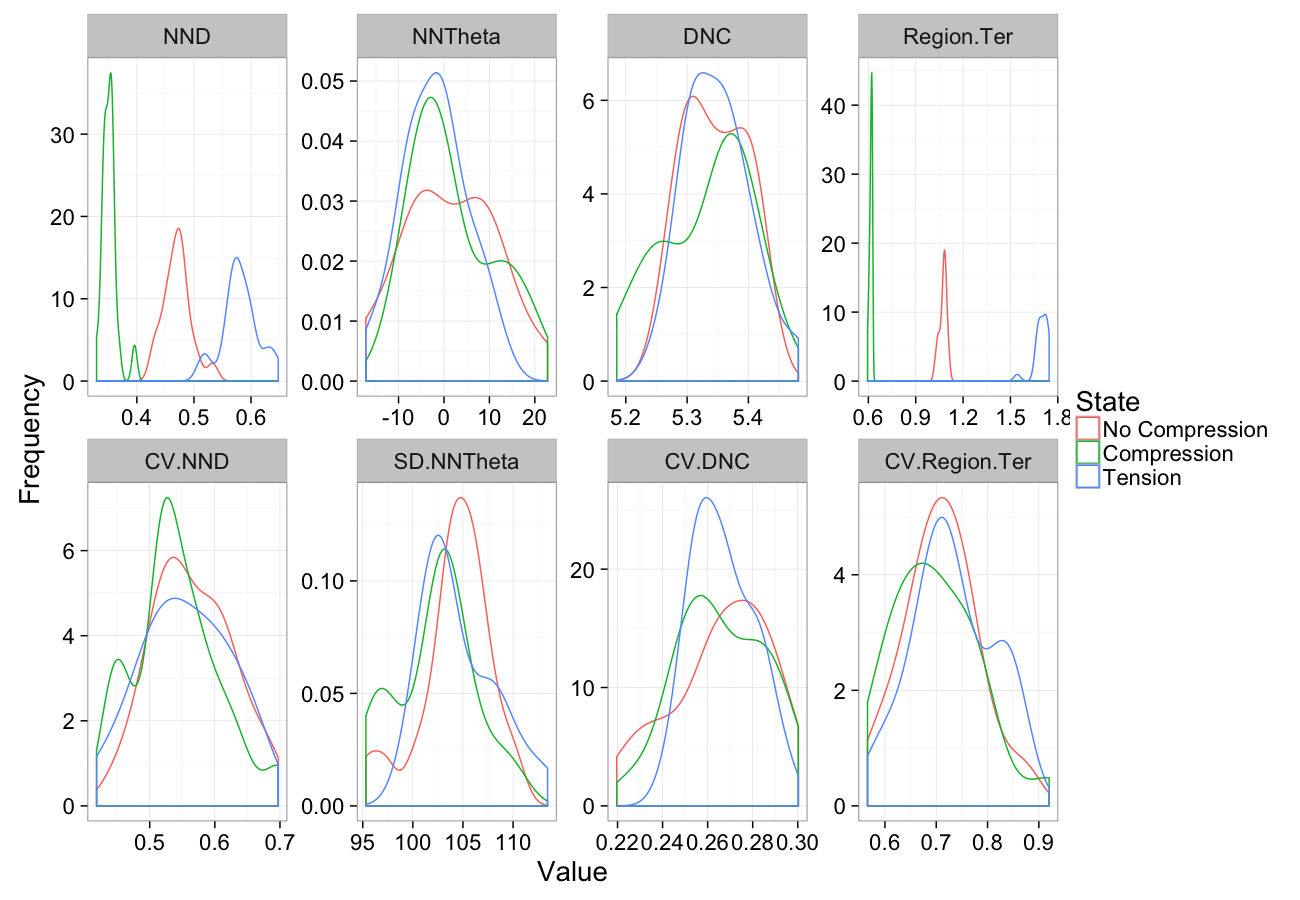
Compression

comp.sim<-rbind(cbind(many.grid(c.pts),system="No Compression"),
                cbind(many.grid(c.pts,trans.fun=function(in.df) comp.fun(0.75,in.df)),system="Compression"),
                cbind(many.grid(c.pts,trans.fun=function(in.df) comp.fun(1.25,in.df)),system="Tension")
                )
ggplot(melt(comp.sim),aes(x=value,color=system))+
  geom_density()+
  facet_wrap(~variable,scales="free",ncol=4)+
  labs(y="Frequency",x="Value",color="State")+
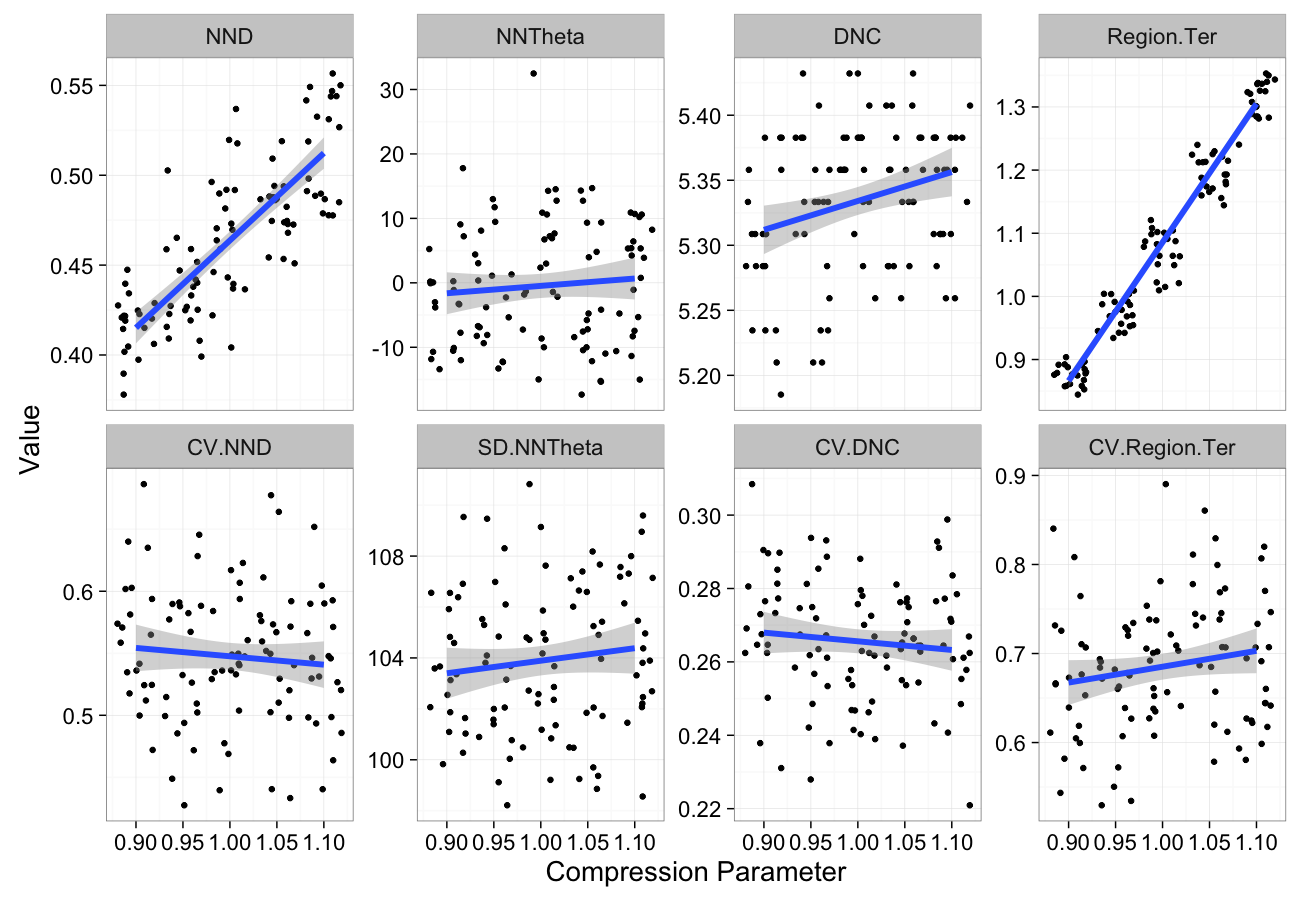
  theme_bw(20)

Compression Sensitivity

comp.data<-ldply(seq(0.9,1.1,length.out=5),function(c.comp) 
  cbind(many.grid(c.pts,trans.fun=function(in.df) comp.fun(c.comp,in.df)),comp=c.comp))


ggplot(melt(comp.data,id.vars=c("comp")),aes(x=comp,y=value))+
  geom_jitter()+
  geom_smooth(method="lm",size=2)+
  labs(y="Value",x="Compression Parameter")+
  facet_wrap(~variable,scale="free_y",ncol=4)+
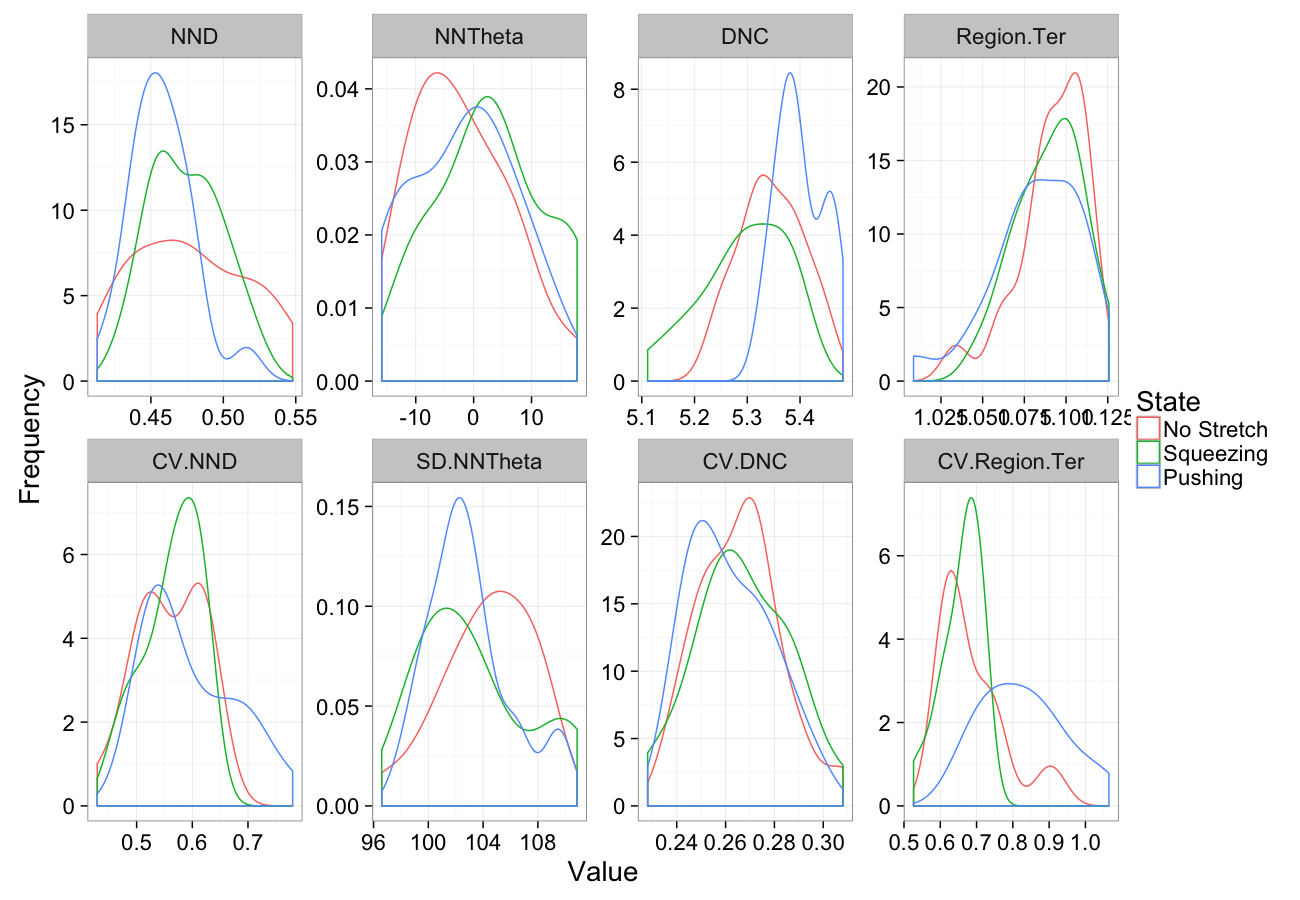
  theme_bw(20)

Stretching

comp.sim<-rbind(cbind(many.grid(c.pts),system="No Stretch"),
                cbind(many.grid(c.pts,trans.fun=function(in.df) stretch.fun(0.8,in.df)),system="Squeezing"),
                cbind(many.grid(c.pts,trans.fun=function(in.df) stretch.fun(1.2,in.df)),system="Pushing")
                )

ggplot(melt(comp.sim),aes(x=value,color=system))+
  geom_density()+
  facet_wrap(~variable,scales="free",ncol=4)+
  labs(y="Frequency",x="Value",color="State")+
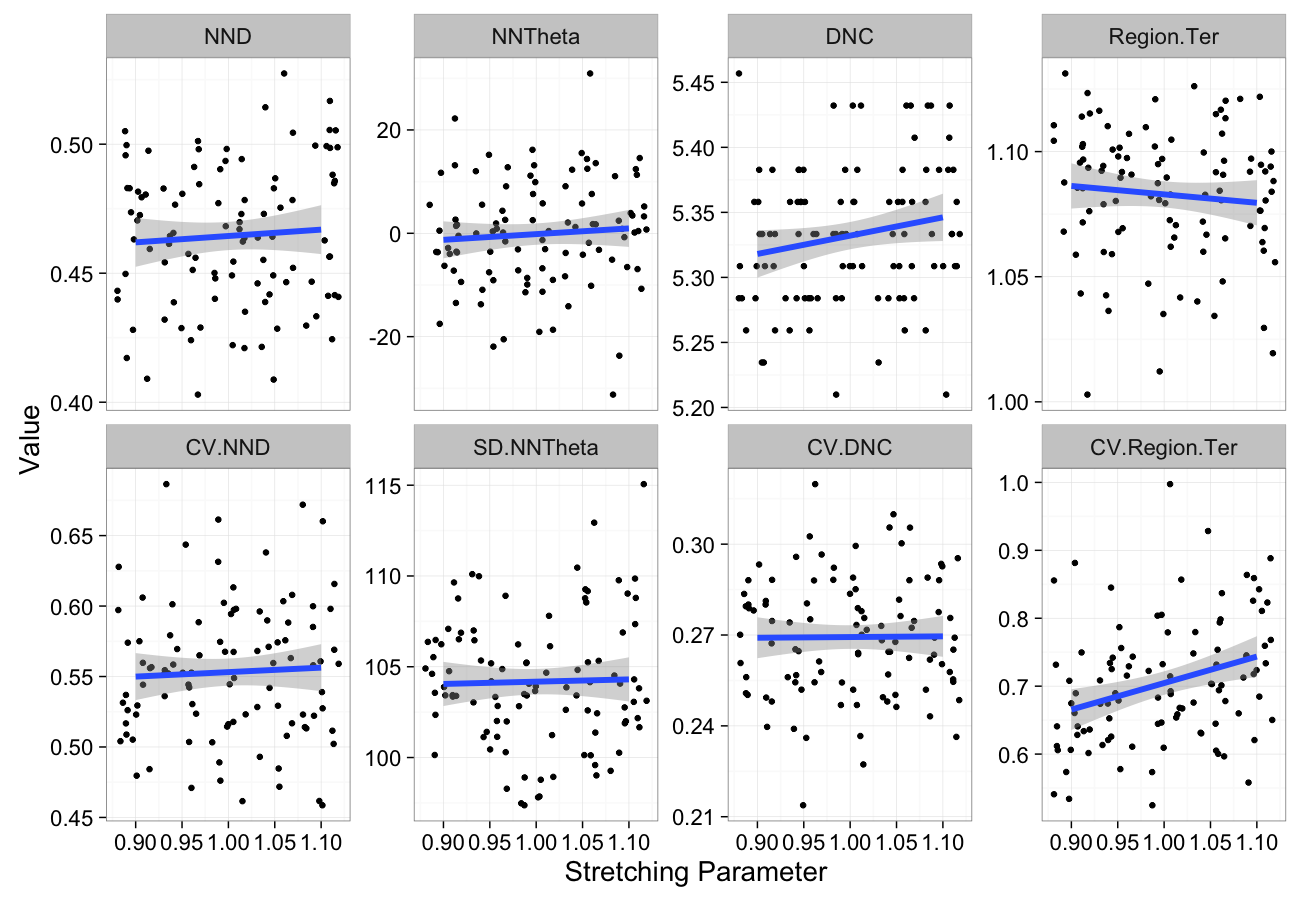
  theme_bw(20)

Stretching Sensitivity

stretch.data<-ldply(seq(0.9,1.1,length.out=5),function(c.stretch) 
  cbind(many.grid(c.pts,trans.fun=function(in.df) stretch.fun(c.stretch,in.df)),stretch=c.stretch))

ggplot(melt(stretch.data,id.vars=c("stretch")),aes(x=stretch,y=value))+
  geom_jitter()+
  geom_smooth(method="lm",size=2)+
  labs(y="Value",x="Stretching Parameter")+
  facet_wrap(~variable,scale="free_y",ncol=4)+
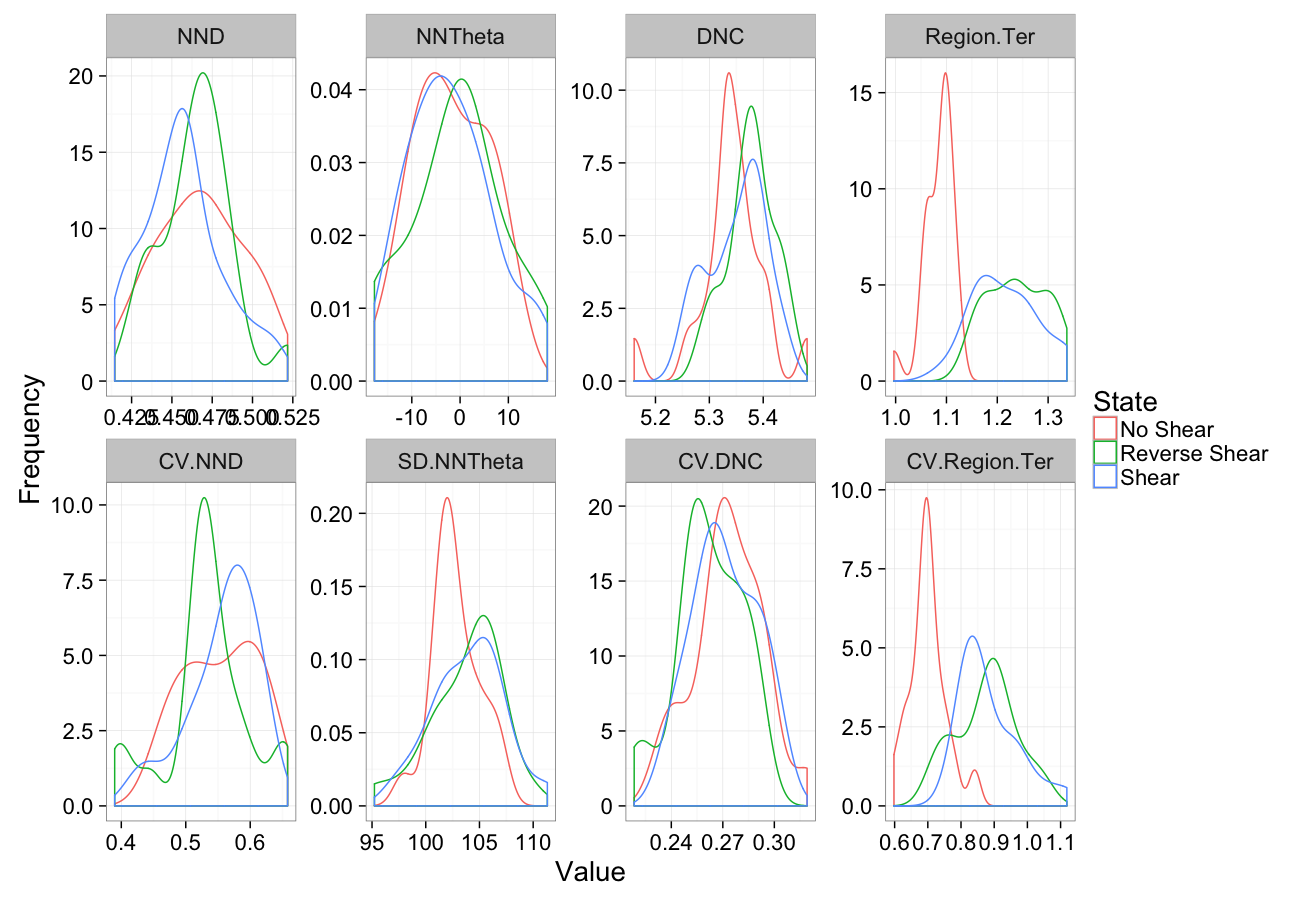
  theme_bw(20)

Shearing

comp.sim<-rbind(cbind(many.grid(c.pts),system="No Shear"),
                cbind(many.grid(c.pts,trans.fun=function(in.df) shear.fun(-0.5,in.df)),system="Reverse Shear"),
                cbind(many.grid(c.pts,trans.fun=function(in.df) shear.fun(0.5,in.df)),system="Shear")
                )

ggplot(melt(comp.sim),aes(x=value,color=system))+
  geom_density()+
  facet_wrap(~variable,scales="free",ncol=4)+
  labs(y="Frequency",x="Value",color="State")+
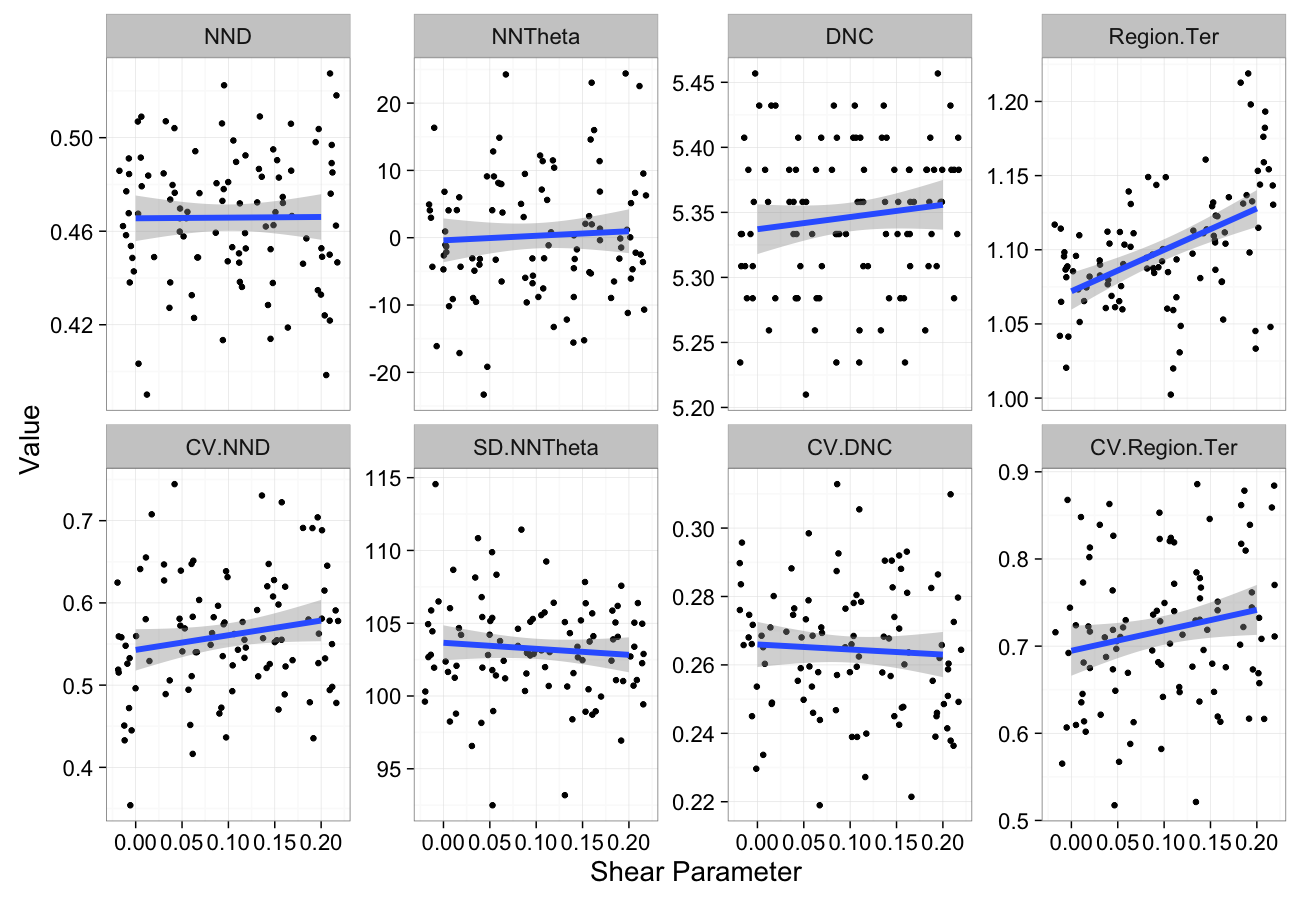
  theme_bw(20)

Shearing Sensitivity

shear.data<-ldply(seq(0,0.2,length.out=5),function(c.shear) 
  cbind(many.grid(c.pts,trans.fun=function(in.df) shear.fun(c.shear,in.df)),shear=c.shear))

ggplot(melt(shear.data,id.vars=c("shear")),aes(x=shear,y=value))+
  geom_jitter()+
  geom_smooth(method="lm",size=2)+
  labs(y="Value",x="Shear Parameter")+
  facet_wrap(~variable,scale="free_y",ncol=4)+
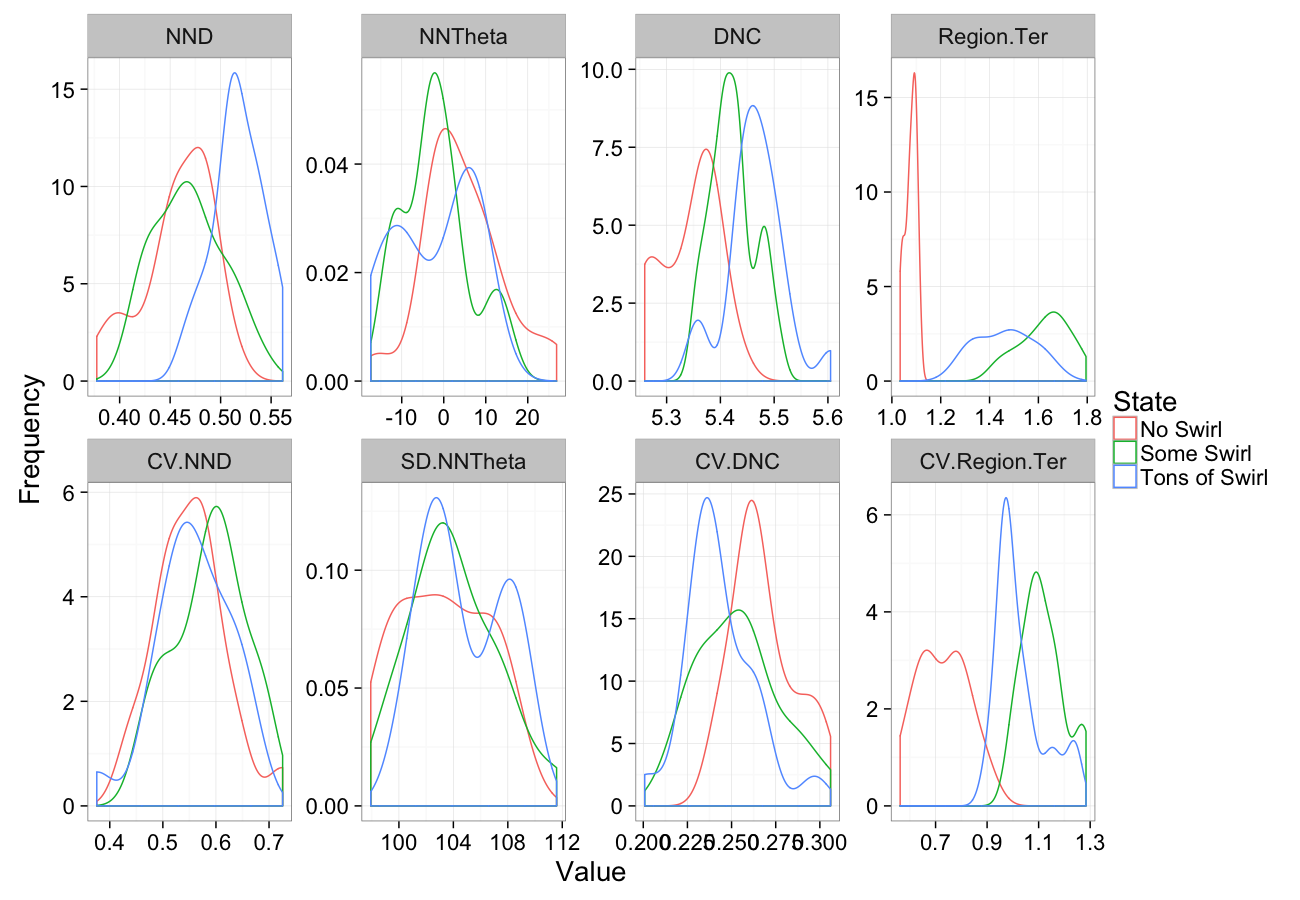
  theme_bw(20)

Swirling

comp.sim<-rbind(cbind(many.grid(c.pts),system="No Swirl"),
                cbind(many.grid(c.pts,trans.fun=function(in.df) swirl.fun(0.5,in.df)),system="Some Swirl"),
                cbind(many.grid(c.pts,trans.fun=function(in.df) swirl.fun(2,in.df)),system="Tons of Swirl")
                )

ggplot(melt(comp.sim),aes(x=value,color=system))+
  geom_density()+
  facet_wrap(~variable,scales="free",ncol=4)+
  labs(y="Frequency",x="Value",color="State")+
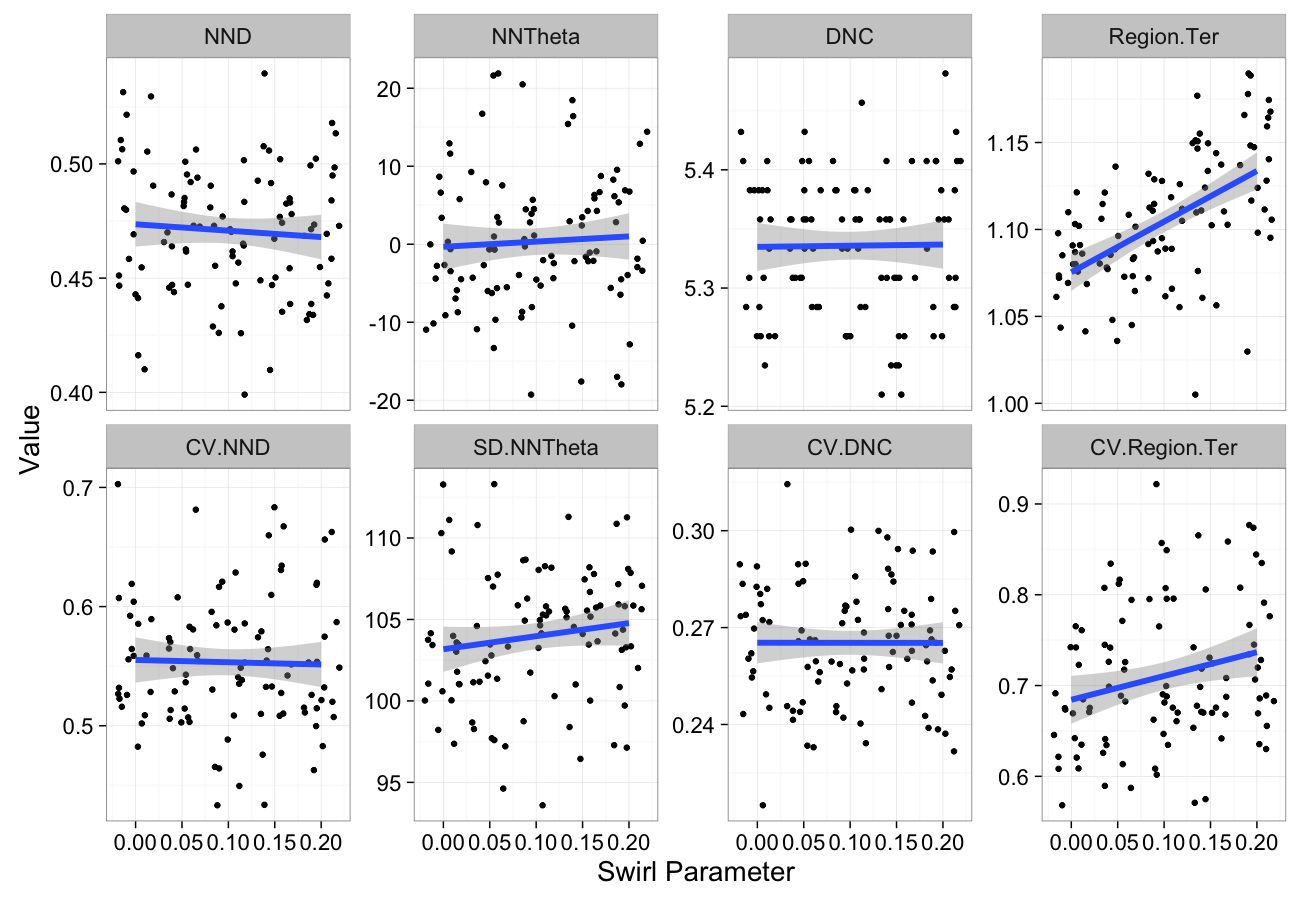
  theme_bw(20)

Swirling Sensitivity

swirl.data<-ldply(seq(0,0.2,length.out=5),function(c.swirl) 
  cbind(many.grid(c.pts,trans.fun=function(in.df) shear.fun(c.swirl,in.df)),swirl=c.swirl))

ggplot(melt(swirl.data,id.vars=c("swirl")),aes(x=swirl,y=value))+
  geom_jitter()+
  geom_smooth(method="lm",size=2)+
  labs(y="Value",x="Swirl Parameter")+
  facet_wrap(~variable,scale="free_y",ncol=4)+
  theme_bw(20)

Self-Avoiding

From the nearest neighbor distance metric, we can create a scale-free version of the metric which we call self-avoiding coefficient or grouping.

The metric is the ratio of

observed nearest neighbor distance NND
the expected mean nearest neighbor distance (r₀) for a random point distribution (Poisson Point Process) with the same number of points (N.Obj) per volume (Total.Volume).
$r_0=\sqrt[3]{\frac{\textrm{Total.Volume}}{2\pi \textrm{ N.Obj}}}$

Using the territory we defined earlier (Region area/volume) we can simplify the definition to

$r_0=\sqrt[3]{\frac{\bar{\textrm{Ter}}}{2\pi}}$

$\textrm{SAC} = \frac{\textrm{NND}}{\sqrt[3]{\frac{\bar{\textrm{Ter}}}{2\pi}}}$

Distribution Tensor

So the information we have is 3D why are we taking single metrics (distance, angle, volume) to quantify it.

Shouldn’t we use 3D metrics with 3D data?
Just like the shape tensor we covered before, we can define a distribution tensor to characterize the shape of the distribution.
The major difference instead of constituting voxels we use edges
an edge is defined from the Delaunay triangluation
it connects two neighboring bubbles together

We can calculate distribution for a single bubble by taking all edges that touch the object or from a region by finding all edges inside that region

We start off by calculating the covariance matrix from the list of edges $\vec{v}_{ij}$ in a given volume 𝒱

$\vec{v}_{ij} = \vec{\textrm{COV}}(i)-\vec{\textrm{COV}}(j)$

$COV(\mathcal{V}) = \frac{1}{N} \sum_{\forall \textrm{COM}(i) \in \mathcal{V}} \begin{bmatrix} \vec{v}_x\vec{v}_x & \vec{v}_x\vec{v}_y & \vec{v}_x\vec{v}_z\\ \vec{v}_y\vec{v}_x & \vec{v}_y\vec{v}_y & \vec{v}_y\vec{v}_z\\ \vec{v}_z\vec{v}_x & \vec{v}_z\vec{v}_y & \vec{v}_z\vec{v}_z \end{bmatrix}$

Distribution Tensor (continued)

We then take the eigentransform of this array to obtain the eigenvectors (principal components, $\vec{\Lambda}_{1\cdots 3}$) and eigenvalues (scores, λ_1⋯3)

$COV(I_{id}) \longrightarrow \underbrace{\begin{bmatrix} \vec{\Lambda}_{1x} & \vec{\Lambda}_{1y} & \vec{\Lambda}_{1z} \\ \vec{\Lambda}_{2x} & \vec{\Lambda}_{2y} & \vec{\Lambda}_{2z} \\ \vec{\Lambda}_{3x} & \vec{\Lambda}_{3y} & \vec{\Lambda}_{3z} \end{bmatrix}}_{\textrm{Eigenvectors}} * \underbrace{\begin{bmatrix} \lambda_1 & 0 & 0 \\ 0 & \lambda_2 & 0 \\ 0 & 0 & \lambda_3 \end{bmatrix}}_{\textrm{Eigenvalues}} * \underbrace{\begin{bmatrix} \vec{\Lambda}_{1x} & \vec{\Lambda}_{1y} & \vec{\Lambda}_{1z} \\ \vec{\Lambda}_{2x} & \vec{\Lambda}_{2y} & \vec{\Lambda}_{2z} \\ \vec{\Lambda}_{3x} & \vec{\Lambda}_{3y} & \vec{\Lambda}_{3z} \end{bmatrix}^{T}}_{\textrm{Eigenvectors}}$
The principal components tell us about the orientation of the object and the scores tell us about the corresponding magnitude (or length) in that direction.

Distribution Anisotropy

Visual example

Tensor represents the average spacing between objects in each direction ≈ thickness of background.
Its interpretation is more difficult since it doesn’t represent a real object

Distribution Tensor

From this tensor we can define an anisotropy in the same manner as we defined for shapes. The anisotropy defined as before
$Aiso = \frac{\text{Longest Side}-\text{Shortest Side}}{\text{Longest Side}}$

An isotropic distribution tensor indicates the spacing between objects is approximately the same in every direction
Does not mean a grid, organized, or evenly spaced!
Just the same in every direction
Anisotropic distribution tensor means the spacing is smaller in one direction than the others
Can be regular or grid-like
Just closer on one direction

Distribution Oblateness

Distribution Tensor

From this tensor we can also define oblateness in the same manner as we defined for shapes. The oblateness is also defined as before as a type of anisotropy

$\textrm{Ob} = 2\frac{\lambda_{2}-\lambda_{1}}{\lambda_{3}-\lambda_{1}}-1$

Indicates the pancakeness of the distribution
Oblate means it is very closely spaced in one direction and far in the other two
strand-like structure
Prolate means it is close in two directions and far in the other
sheet-like structure

Orientation

The shape tensor provides for each object 3 possible orientations (each of the eigenvectors). For simplicity we will take the primary direction (but the others can be taken as well, and particularly in oblate or pancake shaped objects the first is probably not the best choice!)

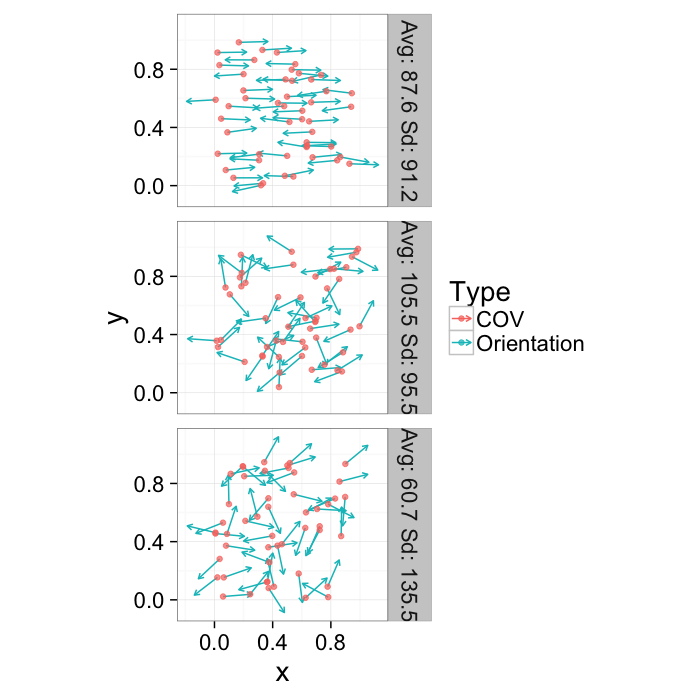
opt.maker<-function(n.pts,rn.fun=function(pts) runif(pts,min=0,max=1),th.amp=0,...) {
  th.val<-rnorm(n.pts,sd=th.amp)+pi*round(runif(n.pts))
  data.frame(x=rn.fun(n.pts),y=rn.fun(n.pts),
             xv=cos(th.val),yv=sin(th.val),
             th.amp=th.amp,n.pts=n.pts,
             Angle.Variability=180/pi*th.amp,
             Mean.Angle=mean(180/pi*th.val),
             Sd.Angle=sd(180/pi*th.val),
             label=paste("Avg:",round(mean(180/pi*th.val)*10)/10,"Sd:",round(sd(180/pi*th.val)*10)/10),...)
}
or.data<-ldply(seq(1e-1,pi/1.5,length.out=3),function(noise) opt.maker(50,th.amp=noise))

ggplot(or.data,
       aes(x,y,xend=x+0.2*xv,yend=y+0.2*yv))+
  geom_segment(aes(color="Orientation"),arrow=arrow(length = unit(0.15,"cm")))+
  geom_point(aes(color="COV"),alpha=0.7)+
  facet_grid(label~.)+
  coord_equal()+
  labs(color="Type")+
  theme_bw(20)

Orientation

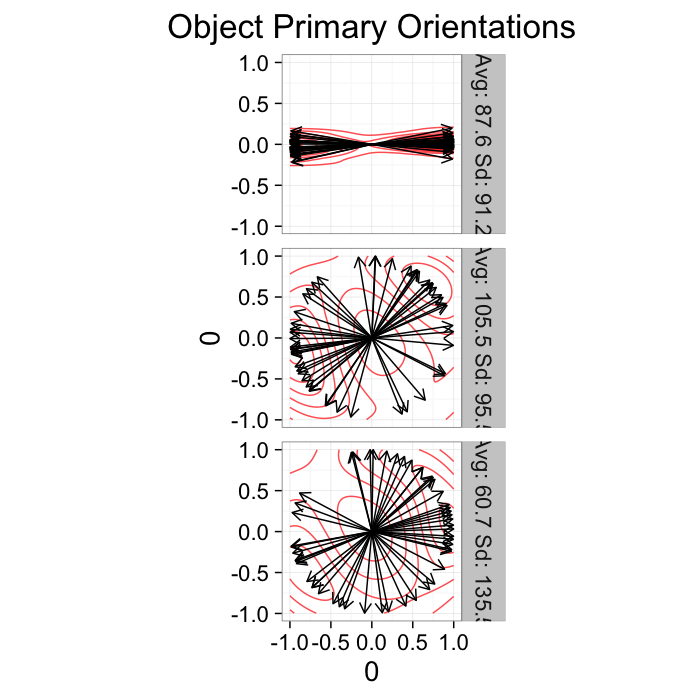
Since orientation derived from a shape tensor / ellipsoid model has no heads or tails. The orientation is only down to a sign → = =← and ↑ = =↓.

ggplot(or.data,
       aes(x=0,y=0,xend=xv,yend=yv))+
    geom_density2d(aes(x=xv,y=yv),color="red",alpha=0.7)+
  geom_segment(arrow=arrow(length = unit(0.3,"cm")))+
   facet_grid(label~.)+
    coord_equal()+
  labs(title="Object Primary Orientations")+guides(color=F)+
  theme_bw(20)

This means calculating the average and standard deviation are very poor desciptors of the actual dataset. The average for all samples below is around 90 (vertical) even though almost no samples are vertical and the first sample shows a very high (90) standard deviation even though all the samples in reality have the same orientation.

kable(ddply(or.data[,c("Angle.Variability","Mean.Angle","Sd.Angle")],.(Angle.Variability),function(x) x[1,]))

Angle.Variability	Mean.Angle	Sd.Angle
5.729578	87.55365	91.23440
62.864789	105.46863	95.53875
120.000000	60.74144	135.54764

The problem can be dealt with by using the covariance matrix which takes advantage of the products which makes the final answer independent of sign.

Alignment Tensor

We can again take advantage of the versatility of a tensor representation for our data and use an alignment tensor.

The same as all of the tensors we have introduced
Except we use the primary orientation instead of voxel positions (shape) or edges (distribution)
Similar to distribution it is calculated for a volume (𝒱) or region and is meaningless for a single object

$\vec{v}_{i} = \vec{\Lambda_1}(i)$

$COV = \frac{1}{N} \sum_{\forall \textrm{COM}(i) \in \mathcal{V}} \begin{bmatrix} \vec{v}_x\vec{v}_x & \vec{v}_x\vec{v}_y & \vec{v}_x\vec{v}_z\\ \vec{v}_y\vec{v}_x & \vec{v}_y\vec{v}_y & \vec{v}_y\vec{v}_z\\ \vec{v}_z\vec{v}_x & \vec{v}_z\vec{v}_y & \vec{v}_z\vec{v}_z \end{bmatrix}$

Alignemnt Tensor

Alignment Tensor: Example

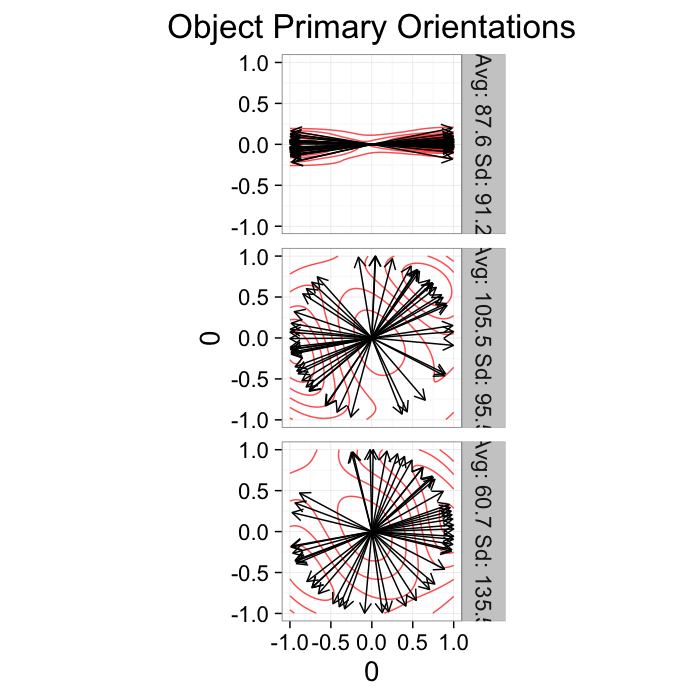
Using the example from before

ggplot(or.data,
       aes(x=0,y=0,xend=xv,yend=yv))+
    geom_density2d(aes(x=xv,y=yv),color="red",alpha=0.7)+
  geom_segment(arrow=arrow(length = unit(0.3,"cm")))+
   facet_grid(label~.)+
    coord_equal()+
  labs(title="Object Primary Orientations")+guides(color=F)+
  theme_bw(20)

Show some tensor stuff here

align.func<-function(in.data) ddply(in.data,
                              .(label),
                              function(csubset) {
                                # calculate the ~covariance of the orientations
                                tmat<-as.matrix(csubset[,c("xv","yv")])
                                cmat<-t(tmat) %*% tmat # cov without mean subtraction
                                # calculate the eigen-transform
                                ceigen<-eigen(cmat)
                                # get the first eigenvector
                                fvec<-ceigen$vectors[,1]
                                # calculate the anisotropy
                                aiso<-(max(ceigen$values)-min(ceigen$values)) / max(ceigen$values)
                                cbind(
                                  csubset,
                                  data.frame(
                                    a.x=fvec[1],a.y=fvec[2],
                                    mn.angle=180/pi*atan2(mean(csubset$yv),mean(csubset$xv)),
                                    Alignment=aiso*100,
                                    alabel=paste("Align =",round(aiso*100)))
                                  )
                              }
                      )
alignment.results<-align.func(or.data)

Alignment Anisotropy

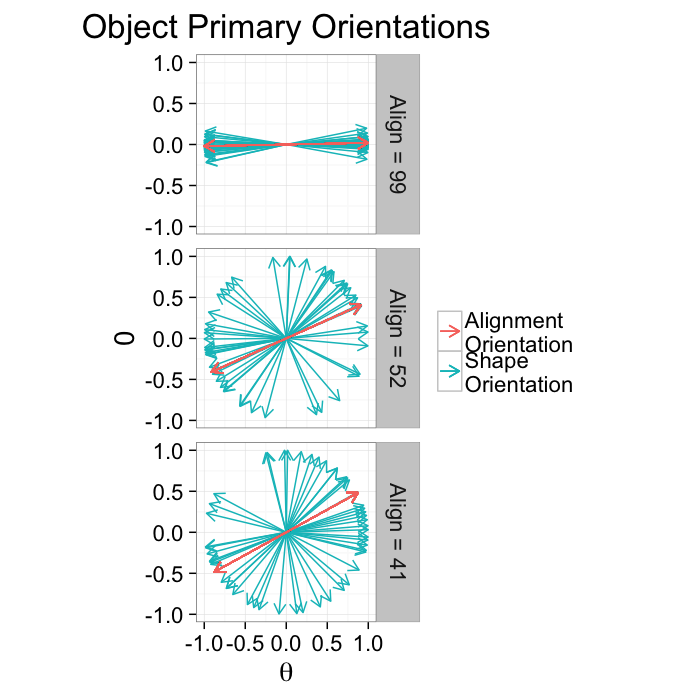
Anisotropy for alignment can be summarized as degree of alignment since very anisotropic distributions mean the objects are aligned well in the same direction while an isotropic distribution means the orientations are random. Oblateness can also be defined but is normally not particularly useful.

$Aiso = \frac{\text{Longest Side}-\text{Shortest Side}}{\text{Longest Side}}$

Alignemnt Tensor

Alignment Anisotropy Applied

ggplot(alignment.results,
       aes(x=0,y=0,xend=xv,yend=yv))+
  geom_segment(aes(color="Shape\nOrientation"),arrow=arrow(length = unit(0.3,"cm")))+
  geom_segment(aes(xend=a.x,yend=a.y,color="Alignment\nOrientation"),
               arrow=arrow(length = unit(0.3,"cm")))+
  geom_segment(aes(xend=-a.x,yend=-a.y,color="Alignment\nOrientation"),
               arrow=arrow(length = unit(0.3,"cm")))+
  facet_grid(alabel~.)+
  coord_equal()+
  labs(title="Object Primary Orientations",color="",x=expression(theta))+
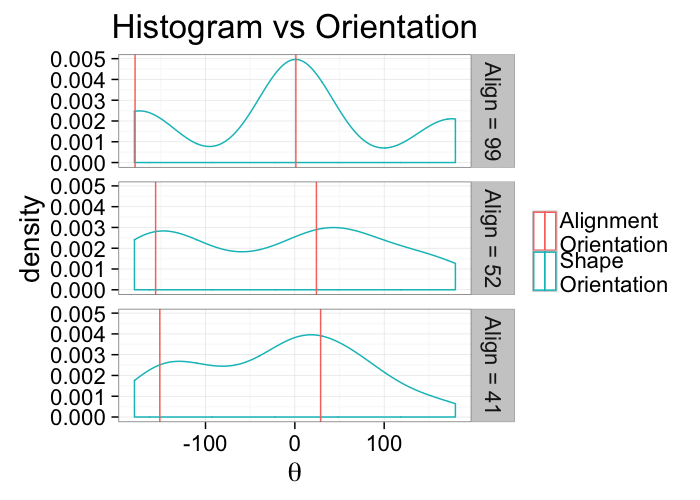
  theme_bw(20)

ggplot(alignment.results,
       aes(x=180/pi*atan2(yv,xv)))+
  geom_density(aes(color="Shape\nOrientation"))+
  geom_vline(aes(xintercept=180/pi*atan2(a.y,a.x),color="Alignment\nOrientation"))+
  geom_vline(aes(xintercept=180/pi*atan2(-a.y,-a.x),color="Alignment\nOrientation"))+
  facet_grid(alabel~.)+
  labs(title="Histogram vs Orientation",color="",x=expression(theta))+
  theme_bw(20)

kable(ddply(alignment.results[,c("Angle.Variability","Mean.Angle","Sd.Angle","Alignment")],.(Angle.Variability),function(x) x[1,]))

Angle.Variability	Mean.Angle	Sd.Angle	Alignment
5.729578	87.55365	91.23440	99.20915
62.864789	105.46863	95.53875	52.40952
120.000000	60.74144	135.54764	41.31333

Alignment for many samples

or.data<-ldply(seq(2e-1,pi/2,length.out=16),function(noise) opt.maker(1000,th.amp=noise))
alignment.results<-align.func(or.data)
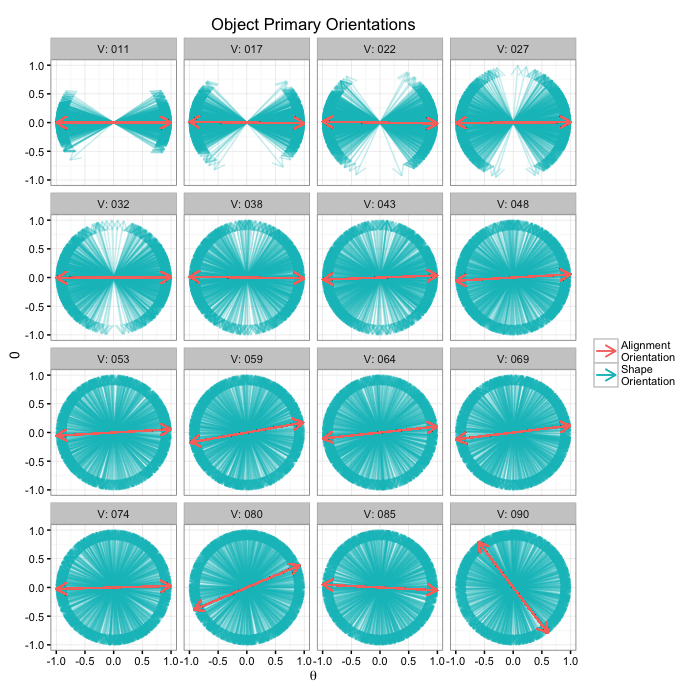
alignment.results$flabel<-paste("V:",sprintf("%03d",round(alignment.results$Angle.Variability)))
ggplot(alignment.results,
       aes(x=0,y=0,xend=xv,yend=yv))+
  geom_segment(aes(color="Shape\nOrientation"),arrow=arrow(length = unit(0.3,"cm")),alpha=0.25)+
  geom_segment(aes(xend=a.x,yend=a.y,color="Alignment\nOrientation"),
               arrow=arrow(length = unit(0.3,"cm")))+
  geom_segment(aes(xend=-a.x,yend=-a.y,color="Alignment\nOrientation"),
               arrow=arrow(length = unit(0.3,"cm")))+
  facet_wrap(~flabel)+
  coord_equal()+
  labs(title="Object Primary Orientations",color="",x=expression(theta))+
  theme_bw(10)

Angle Accuracy

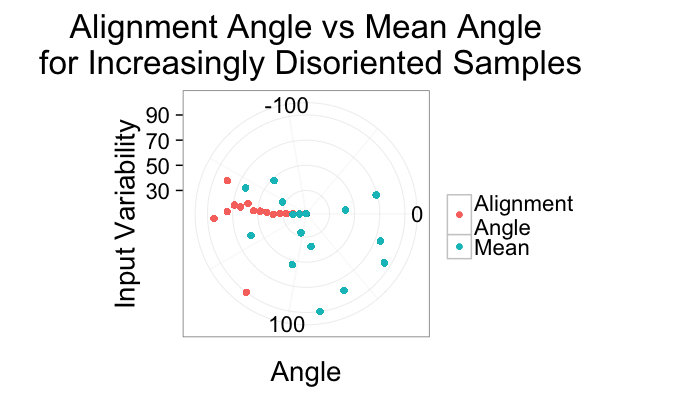
ggplot(alignment.results,aes(x=Angle.Variability))+
  geom_point(aes(y=180/pi*atan2(a.y,a.x),color="Alignment\nAngle"))+
  geom_point(aes(y=mn.angle,color="Mean"))+
  coord_polar(theta="y",start=-pi/2)+
  ylim(-180,180)+
  labs(title="Alignment Angle vs Mean Angle\n for Increasingly Disoriented Samples",color="",
       y="Angle",x="Input Variability")+
  theme_bw(20)

Variability Accuracy

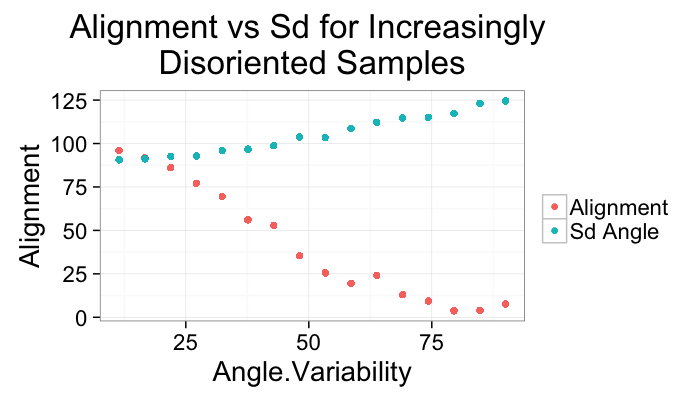
ggplot(alignment.results,aes(x=Angle.Variability))+
  geom_point(aes(y=Alignment,color="Alignment"))+
  geom_point(aes(y=Sd.Angle,color="Sd Angle"))+
  labs(title="Alignment vs Sd for Increasingly \nDisoriented Samples",color="")+
  theme_bw(20)

Other Approaches

K-Means

K-Means can also be used to classify the point-space itself after shape analysis. It is even better suited than for images because while most images are only 2 or 3D the shape vector space can be 50-60 dimensional and is inherently much more difficult to visualize.

2 Point Correlation Functions

For a wider class of analysis of spatial distribution, there exist a class a functions called N-point Correlation Functions

given a point of type A at $\vec{x}$
what is the probability of B at $\vec{x}+\vec{r}$
How is it useful
A simple analysis can be used to see the spacing of objects (peaks in the $F(\vec{r})$ function, A and B are the same phase).
Where are cells located in reference to canals (peaks in $F(\vec{r})$ function, A is a point inside a canal B is the cells)