Quantitative Big Imaging
Kevin Mader
27 March 2014
ETHZ: 227-0966-00L
Analysis of Complex Objects
Course Outline
- 20th February - Introductory Lecture
- 27th February - Filtering and Image Enhancement (A. Kaestner)
- 6th March - Basic Segmentation, Discrete Binary Structures
- 13th March - Advanced Segmentation
- 20th March - Analyzing Single Objects
- 27th March - Analyzing Complex Objects
- 3rd April - Spatial Distribution
- 10th April - Statistics and Reproducibility
- 17th April - Dynamic Experiments
- 8th May - Big Data
- 15th May - Guest Lecture - In-Operando Imaging of Batteries (V. Wood)
- 22th May - Project Presentations
Literature / Useful References
Books
Papers / Sites
- Thickness
- [1] Hildebrand, T., & Ruegsegger, P. (1997). A new method for the model-independent assessment of thickness in three-dimensional images. Journal of Microscopy, 185(1), 67–75. doi:10.1046/j.1365-2818.1997.1340694.x
- Curvature
- http://mathworld.wolfram.com/MeanCurvature.html
- [2] “Computation of Surface Curvature from Range Images Using Geometrically Intrinsic Weights”*, T. Kurita and P. Boulanger, 1992.
Previously on QBI ...
- Image Enhancment
- Highlighting the contrast of interest in images
- Minimizing Noise
- Segementation
- Understanding value histograms
- Dealing with multi-valued data
- Automatic Methods
- Hysteresis Method, K-Means Analysis
- Regions of Interest
- Contouring
- Component Labeling
- Single Shape Analysis
Outline
- Motivation (Why and How?)
- What are Distance Maps?
- Skeletons
- Tortuosity
- What are thickness maps?
- Thickness with Skeletons
- Watershed Segmentation
- Connected Objects
- Curvature
- Characteristic Shapes
Learning Objectives
Motivation (Why and How?)
- How do we measure distances between many objects?
How can we extract topology of a structure?
How can we measure sizes in complicated objects?
How do we measure sizes relavant for diffusion or other local processes?
How do we identify seperate objects when they are connected?
How do we investigate surfaces in more detail and their shape?
How can we compare shape of complex objects when they grow?
- Are there characteristic shape metrics?
What did we want in the first place
To simplify our data, but an ellipse model is too simple for many shapes
So while bounding box and ellipse-based models are useful for many object and cells, they do a very poor job with the sample below.
Why
- We assume an entity consists of connected pixels (wrong)
- We assume the objects are well modeled by an ellipse (also wrong)
What to do?
- Is it 3 connected objects which should all be analzed seperately?
- If we could divide it, we could then analyze each spart as an ellipse
- Is it one network of objects and we want to know about the constrictions?
- Is it a cell or organelle with docking sites for cell?
- Neither extents nor anisotropy are very meaningful, we need a more specific metric which can characterize
Distance Maps: What are they
A map (or image) of distances. Each point in the map is the distance that point is from a given feature of interest (surface of an object, ROI, center of object, etc)
Definition
If we start with an image as a collection of points divided into two categories
- \( Im(x,y)= \) {Foreground, Background}
- We can define a distance map operator (\( dist \)) that transforms the image into a distance map
\[ dist(\vec{x}) = \textrm{min}(||\vec{x}-\vec{y}|| \forall \vec{y} \in \textrm{Background}) \]
We will use Euclidean distance \( ||\vec{x}-\vec{y}|| \) for this class but there are other metrics which make sense when dealing with other types of data like Manhattan/City-block or weighted metrics.
Distance Maps: Types
Using this rule a distance map can be made for the euclidean metric
Similarly the Manhattan or city block distance metric can be used where the distance is defined as \[ \sum_{i} |\vec{x}-\vec{y}|_i \]
Distance Maps: Precaution
The distance map is one of the crictical points where the resolution of the imaging system is important.
- We measure distances computationally in pixels or voxels
- but for them to have a meaning physically they must be converted
- Isotropic imaging (1 \( \mu \) m x 1\( \mu \) m x 1 \( \mu \) m) is fine
Anisotropic
Ideally
- as part of filtering, resample and convert to an isotropic scale.
If that is not possible
- custom distance map algorithms which use the side-lengths of the voxels to calculate distance rather than assuming 1x1x1
Distance Maps
We can create 2 distance maps
Foreground \( \rightarrow \) Background
- Information about the objects size and interior
Background \( \rightarrow \) Foreground
- Information about the distance / space between objects
Distance Map
One of the most useful components of the distance map is that it is relatively insensitive to small changes in connectivity.
- Component Labeling would find radically different results for these two images
- One has 4 small circles
- One has 1 big blob
Distance Map of Cell
Foreground
Background
Skeletonization / Networks
For some structures like cellular materials and trabecular bone, we want a more detailed analysis than just thickness. We want to know
- which structures are connected
- how they are connected
- express the network in a simple manner
- quantify tortuosity
- branching
Skeletonization
The first step is to take the distance transform the structure \[ I_d(x,y) = \textrm{dist}(I(x,y)) \] We can see in this image there are already local maxima that form a sort of backbone which closely maps to what we are interested in.
By using the laplacian filter as an approximate for the derivative operator which finds the values which high local gradients.
\[ \nabla I_{d}(x,y) = (\frac{\delta^2}{\delta x^2}+\frac{\delta^2}{\delta y^2})I_d \approx \underbrace{\begin{bmatrix} -1 & -1 & -1 \\ -1 & 8 & -1 \\ -1 & -1 & -1 \end{bmatrix}}_{\textrm{Laplacian Kernel}} \otimes I_d(x,y) \]
Creating the skeleton
We can locate the local maxima of the structure by setting a minimum surface distance \[ I_d(x,y)>MIN_{DIST} \] and combining it with a minimum slope value \[ \nabla I_d(x,y) > MIN_{SLOPE} \]
Thresholds
Harking back to our first lectures, this can be seen as a 2D threshold of the entire dataset.
- We first make the dataset into a tuple
\[ \textrm{cImg}(x,y) = \langle \underbrace{I_d(x,y)}_1, \underbrace{\nabla I_d(x,y)}_2 \rangle \]
\[ \textrm{skelImage}(x,y) = \] \[ \begin{cases} 1, & \textrm{cImg}_1(x,y)\geq MIN-DIST \\ & \& \textrm{ cImg}_2(x,y)\geq MIN-SLOPE \\ 0, & \textrm{otherwise} \end{cases} \]
Skeleton: Different Thresholds
Skeleton: Pruning
The structure is a overgrown
- Stricter 'thresholds'
- Sensitive to 'threshold' selection
- Resolution dependent
- Dedicated pruning algorithms
- Ideally model-based
- Minimum branch length
- Minimum branch width
Skeleton: Junctions
With the skeleton which is ideally one voxel thick, we can characterize the junctions in the system by looking at the neighborhood of each voxel.
As with nearly every operation, the neighborhood we define is important and we can see that if we use a box neighborhood vs a cross neighborhood (4 vs 8 adjacent) we count diagonal connections differently
Skeleton: Network Assessment
Once we have classified the skeleton into terminals, segments, and junctions we can analyze the various components and assess metrics like connectivity, branching, and many other.
The easist way is to further process the image by
- component labeling the different segments and joints
- determining the average length of each segment
- number of incoming segments at a given joint
Most of the other metrics can be simply counted
Cross Neighborhood
| label | x |
|---|---|
| Junction | 720 |
| Segment | 332 |
| Terminal | 558 |
Box Neighborhood
| label | x |
|---|---|
| Junction | 1321 |
| Segment | 783 |
| Terminal | 379 |
Skeleton: Tortuosity
One of the more interesting ones in material science is called tortuosity and it is defined as the ratio between the arc-length of a segment and the distance between its starting and ending points. \[ \tau = \frac{L}{C} \]
A high degree of tortuosity indicates that the network is convoluted and is important when estimating or predicting flow rates. Specifically
- in geology it is an indication that diffusion and fluid transport will occur more slowly
- in analytical chemistry it is utilized to perform size exclusion chromatography
- in vascular tissue it can be a sign of pathology.
Thickness Map: What is it?
Thickness is a metric for assessing the size and structure of objects in a very generic manner. For every point \( \vec{x} \) in the image you find the largest sphere which:
- contains that point
- is entirely contained within the object
Taken from [1]
- The image shows a typical object
- The sphere centered at point \( p \) with a radius \( r \) is the largest that fits
Application
- Ideal for spherical and cylindrical objects since it shows their radius
- Also relevant for flow and diffusion since it can highlight bottlenecks in structure
Thickness Map
Thickness Map
Thickness Map From Skeleton
Calculating the distance map by drawing a sphere at each point is very time consuming (\( O(n^3) \)).
- The skeleton (last section) is very closely related to the thickness.
- We found the local maxima in the image using the Laplace
- We can thus grow the Spheres from these points instead of all
- Start by instead of thresholding transforming the image to the distance at each point
\[ \textrm{thSkelImage}(x,y) = \] \[ \begin{cases} \textrm{cImg}_1(x,y) , & \textrm{cImg}_1(x,y)\geq MIN-DIST \\ & \& \textrm{ cImg}_2(x,y)\geq MIN-SLOPE \\ 0, & \textrm{otherwise} \end{cases} \]
From Skeleton vs All Points
user system elapsed
4.366 0.081 4.464
user system elapsed
13.735 0.413 14.224
Statistically Does it Matter
It depends
- Small structures are lost
- They might not have been very important or noisy anyways
- Higher values are very similar
| id | Full Map | Skeleton Map |
|---|---|---|
| Min. | 0.75 | 1.75 |
| 1st Qu. | 2.47 | 2.47 |
| Median | 2.66 | 2.66 |
| Mean | 2.67 | 2.74 |
| 3rd Qu. | 3.01 | 3.01 |
| Max. | 3.20 | 3.20 |
How much can we cut down
user system elapsed
1.813 0.027 1.841
| id | Full Map | Skeleton Map | Tiny Skeleton Map |
|---|---|---|---|
| Min. | 0.75 | 1.75 | 2.02 |
| 1st Qu. | 2.47 | 2.47 | 2.50 |
| Median | 2.66 | 2.66 | 2.66 |
| Mean | 2.67 | 2.74 | 2.77 |
| 3rd Qu. | 3.01 | 3.01 | 3.01 |
| Max. | 3.20 | 3.20 | 3.20 |
Thickness in 3D Images
While the examples and demonstrations so far have been shown in 2D, the same exact technique can be applied to 3D data as well. For example for this liquid foam structure
The thickness can be calculated of the background (air) voxels in the same manner.
With care, this can be used as a proxy for bubble size distribution in systems where all the bubbles are connected to it is difficult to identify single ones.
Watershed
Watershed is a method for segmenting objects without using component labeling.
- It utilizes the shape of structures to find objects
- From the distance map we can make out substructures with our eyes
- But how to we find them?!
Watershed: Flowing Downhill
So we start by distributing pixels all across the image
If any of the neighbors have a higher distance (more downhill) then move to that position
Watershed: More flowing
Watershed: Regrowing
We can then take the points from these basins and regrow them back to their original size and these represent the watershed regions of our image
Curvature
Curvature is a metric related to the surface or interface between phases or objects.
- It is most easily understood in its 1D sense or being the radius of the circle that matchs the local shape of a curve
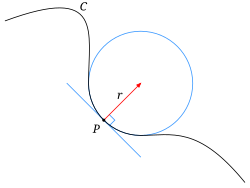
- Mathematically it is defined as
\[ \kappa = \frac{1}{R} \]
- Thus a low curvature means the value means a very large radius and high curvature means a very small radius
Curvature: Surface Normal
In order to meaningfully talk about curvatures of surfaces, we first need to define a consistent frame of reference for examining the surface of an object. We thus define a surface normal vector as a vector oriented orthogonally to the surface away from the interior of the object \( \rightarrow \vec{N} \)
Curvature: 3D
With the notion of surface normal defined (\( \vec{N} \)), we can define many curvatures at point \( \vec{x} \) on the surface.
- This is because there are infinitely many planes which contain both point \( \vec{x} \) and \( \vec{N} \)
- More generally we can define an angle \( \theta \) about which a single plane containing both can be freely rotated
- We can then define two principal curvatures by taking the maximum and minimum of this curve
\[ \kappa_1 = \textrm{max}(\kappa(\theta)) \] \[ \kappa_2 = \textrm{min}(\kappa(\theta)) \]
Mean Curvature
The mean of the two principal curvatures \[ H = \frac{1}{2}(\kappa_1+\kappa_2) \]
Gaussian Curvature
The mean of the two principal curvatures \[ K = \kappa_1\kappa_2 \]
- positive for spheres (or spherical inclusions)
- curvatures agree in sign
- negative for saddles (hyperboloid surfaces)
- curvatures disgree in sign
- 0 for planes
Curvature: 3D Examples
Examining a complex structure with no meaningful ellipsoidal or watershed model. The images themselves show the type of substructures and shapes which are present in the sample.
- gaussian curvature: the comparative amount of surface at, above, and below 0
- from spherical particles into annealed mesh of balls
Characteristic Shape
Characteristic shape can be calculated by measuring principal curvatures and normalizing them by scaling to the structure size. A distribution of these curvatures then provides shape information on a structure indepedent of the size.
For example a structure transitioning from a collection of perfectly spherical particles to a annealed solid will go from having many round spherical faces with positive gaussian curvature to many saddles and more complicated structures with 0 or negative curvature.
Curvature: Take Home Message
It provides another metric for characterizing complex shapes
- Particularly useful for examining interfaces
- Folds, saddles, and many other types of points are not characterized well be ellipsoids or thickness maps
- Provides a scale-free metric for assessing structures
- Can provide visual indications of structural changes
Other Techniques
There are hundreds of other techniques which can be applied to these complicated structures, but they go beyond the scope of this course. Many of them are model-based which means they work well but only for particular types of samples or images. Of the more general techniques several which are easily testable inside of FIJI are
- Directional Analysis = Looking at the orientation of different components using Fourier analysis (Analyze \( \rightarrow \) Directionality)
- Tubeness / Surfaceness (Plugins \( \rightarrow \) Analyze \( \rightarrow \)) characterize binary images and the shape at each point similar to curvature but with a different underlying model
- Fractal Dimensionality = A metric for assessing the structure as you scale up and down by examining various spatial relationships
- Ma, D., Stoica, A. D., & Wang, X.-L. (2009). Power-law scaling and fractal nature of medium-range order in metallic glasses. Nature Materials, 8(1), 30–4. doi:10.1038/nmat2340
- Two (or more) point correlation functions = Used in theoretical material science and physics to describe random materials and can be used to characterize distances, orientations, and organization in complex samples
- Jiao, Y., Stillinger, F., & Torquato, S. (2007). Modeling heterogeneous materials via two-point correlation functions: Basic principles. Physical Review E, 76(3). doi:10.1103/PhysRevE.76.031110
- Andrey, P., Kiêu, K., Kress, C., Lehmann, G., Tirichine, L., Liu, Z., … Debey, P. (2010). Statistical analysis of 3D images detects regular spatial distributions of centromeres and chromocenters in animal and plant nuclei. PLoS Computational Biology, 6(7), e1000853. doi:10.1371/journal.pcbi.1000853
- Haghpanahi, M., & Miramini, S. (2008). Extraction of morphological parameters of tissue engineering scaffolds using two-point correlation function, 463–466. Retrieved from http://portal.acm.org/citation.cfm?id=1713360.1713456